
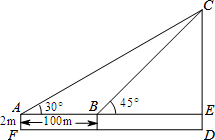
 如图,为了测量建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是2m,请你计算出该建筑物的高度.(结果保留根号)
如图,为了测量建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是2m,请你计算出该建筑物的高度.(结果保留根号)科目:初中数学 来源: 题型:
 如图,在△ABC中,AC=BC,以腰AC、BC为边向外作等边△ACD和△BCE,AE与BD相交于点F,连接CF并延长,交AB于点G.求证:
如图,在△ABC中,AC=BC,以腰AC、BC为边向外作等边△ACD和△BCE,AE与BD相交于点F,连接CF并延长,交AB于点G.求证:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,直线l∥m∥n,等边△ABC的顶点B、C分别在直线n和m上,边BC与直线n所夹的角记为∠1,边AC与直线l所夹的角记为∠2.(友情提示:等边三角形每个内角都等于60°)
如图,直线l∥m∥n,等边△ABC的顶点B、C分别在直线n和m上,边BC与直线n所夹的角记为∠1,边AC与直线l所夹的角记为∠2.(友情提示:等边三角形每个内角都等于60°)查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,点A、B在数轴上分别表示有理数a、b,在数轴上A、B两点之间的距离AB=|a-b|.回答下列问题:
如图,点A、B在数轴上分别表示有理数a、b,在数轴上A、B两点之间的距离AB=|a-b|.回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com