
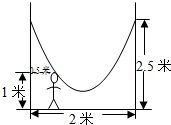
 如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为( )米.
如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为( )米.| A、0.5 | B、0.6 |
| C、1 | D、1.5 |


科目:初中数学 来源: 题型:
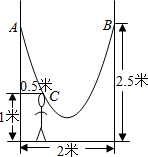
 如图,有一座抛物线形拱桥,已知桥下在正常水位AB时,水面宽8m,水位上升3m,就达到警戒水位CD,这时水面宽4m,若洪水到来时,水位以每小时0.2m的速度上升,求水过警戒水位后几小时淹到桥拱顶.
如图,有一座抛物线形拱桥,已知桥下在正常水位AB时,水面宽8m,水位上升3m,就达到警戒水位CD,这时水面宽4m,若洪水到来时,水位以每小时0.2m的速度上升,求水过警戒水位后几小时淹到桥拱顶.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
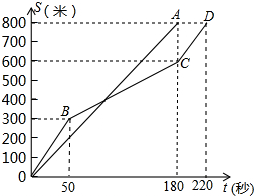 在某市初中学业水平考试体育学科800米能力测试中,某考点同时起跑的甲和乙所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD.下列说法错误的是( )
在某市初中学业水平考试体育学科800米能力测试中,某考点同时起跑的甲和乙所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD.下列说法错误的是( )| A、甲比乙先到达终点 |
| B、跑步过程中甲的速度不变 |
| C、起跑后400米内,乙始终在甲的前面 |
| D、在起跑后180米时,甲乙两人相遇 |
查看答案和解析>>
科目:初中数学 来源: 题型:
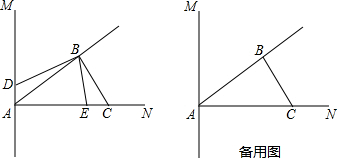
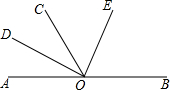 如图:O为直线AB上的一点,∠AOC=60°,OD平分∠AOC,∠DOC与∠COE互余,
如图:O为直线AB上的一点,∠AOC=60°,OD平分∠AOC,∠DOC与∠COE互余,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com