
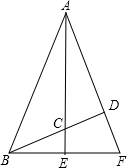
 如图,在△ABC中,延长BC到D,延长AC到E,AD与BE相交于点F,∠ABC=45°,试选取下列条件中的两个作为题设,另一个作为结论组成一个正确命题,①AD⊥BD;②AE⊥BF;③AC=BF.
如图,在△ABC中,延长BC到D,延长AC到E,AD与BE相交于点F,∠ABC=45°,试选取下列条件中的两个作为题设,另一个作为结论组成一个正确命题,①AD⊥BD;②AE⊥BF;③AC=BF.
|


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| a |
| 1 |
| a |
| 1 |
| a2 |
| 1 |
| a4 |
| 1 |
| a |
| a2+5a+1 |
| a2-2a+1 |
| a2 |
| a4+1 |
| a2 |
| a4+a2+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:| 每月用气量 | 单价(元/m3) |
| 不超出75m3的部分 | 2 |
| 超出75m3不超出125m3的部分 | a |
| 超出125m3的部分 | a+0.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
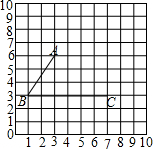 已知如图,请根据图形回答问题.
已知如图,请根据图形回答问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com