【题目】如图 1，在平面直角坐标系中，A,B,D 三点的坐标是（0，2），（-2,0），（1,0），点C 是 x 轴下方一点，且 CD⊥AD,∠BAD+∠BCD=180°，AD=CD

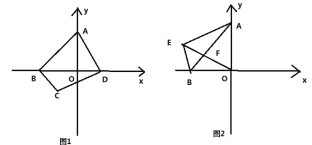
(1)求证：BD 平分∠ABC

(2)求四边形 ABCD 的面积

(3)如图 2，BE 是∠ABO 的邻补角的平分线，连接 AE,OE 交 AB 于点 F，若∠AEO=45°，求证：AF=AO.

参考答案：

【答案】(1)证明见解析；（2）；（3）证明见解析；

【解析】

（1）过C作DM⊥BD于M，根据AAS判定△CDM≌△DOA，通过线段和差推出BM=MC=1得出∠CBD=45°进而得到∠CBD=∠ABO=45°即可证BD 平分∠ABC；

（2）将，再根据三角形的面积公式计算即可；
（3）过点E作作EH⊥x轴于点H，EG⊥BC于点G，根据角平分线的性质得到EH=EG，证明△EAG≌△EOH，得到EA=EO，根据等腰三角形的判定定理解答．

证明：（1）∵A(0,2)B(-2,0)D(1,0)
∴OA=OB=2,OD=1

∴∠ABO=∠BAO=45°
过C作DM⊥BD于M
∴∠CMD=90°
∴∠1+∠3=90°
∵CD⊥AD
∴∠ADC=90°
∴∠1+∠2=90°
∴∠2=∠3

又∵CD=AD，∠CMD=∠AOD =90°

∴△CDM≌△DOA
∴CM=OD=1，MD=AO=2

∴OM=1

∴BM=1

∴BM=MC=1

∴∠CBD=45°

∴∠CBD=∠ABO=45°

∴BD 平分∠ABC

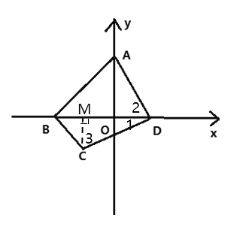
(2)由（1）得A(0,2),B(-2,0),C(-1,-1),M(-1,0)

∴BD=3，AO=2,CM=1

∴

∴

(3)过点E作EH⊥x轴于点H，EG⊥BA于点G，

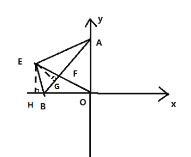
∴∠EHO=∠EGA =90°

∵E点在∠ABO的邻补角的平分线上，EH⊥HO，EG⊥BA

∴EH=EG，

∵∠ABO=∠AEO=45，

∴∠EAG=∠EOH，

在△EAG和EOH中，

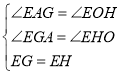
∴△EAG≌△EOH(AAS)，

∴EA=EO，

∵∠AEO=45°，

∴∠EAO=∠EOA=67.5°,

∵∠OAB=45°，

∴∠AFO=180°-∠OAB-∠AOE=67.5°

∴∠AOE=∠AFO=67.5°，

∴AF=AO

关闭