
【题目】已知:在平面直角坐标系中,点A、B的坐标分别是(a,0),(b,0)且![]() +|b-2|=0.
+|b-2|=0.
(1)求a、b的值;
(2)在y轴上是否存在点C,使三角形ABC的面积是12?若存在,求出点C的坐标;若不存在,请说明理由.
(3)已知点P是y轴正半轴上一点,且到x轴的距离为3,若点P沿平行于x轴的负半轴方向以每秒1个单位长度平移至点Q,当运动时间t为多少秒时,四边形ABPQ的面积S为15个平方单位?写出此时点Q的坐标. 
【答案】(1)a=-4,b=2;(2)点C的坐标为(0,4)或(0,-4);(3)点P沿x轴负半轴方向以每秒1个单位长度平移至点Q,点Q的坐标为(-4,3).
【解析】试题分析:(1)根据二次根式与绝对值的非负性可得a+4=0,b-2=0,解得a=-4,b=2;
(2)设点C到x轴的距离为h,利用三角形的面积公式可解得h=4,要考虑点C在y轴正半轴与负半轴两种情况;
(3)先根据四边形ABPQ的面积积S=![]() (6+PQ)×3=15解得PQ=4,再求得点Q的坐标为(-4,3).
(6+PQ)×3=15解得PQ=4,再求得点Q的坐标为(-4,3).
试题解析:(1)根据题意,得
a+4=0,b-2=0,
解得a=-4,b=2;
(2)存在.设点C到x轴的距离为h,
则S△ABC=![]() ABh=
ABh=![]() ×6h=12解得h=4,
×6h=12解得h=4,
所以点C的坐标为(0,4)或(0,-4);
(3)四边形ABPQ的面积S=![]() (6+PQ)×3=15解得PQ=4.
(6+PQ)×3=15解得PQ=4.
点P沿x轴负半轴方向以每秒1个单位长度平移至点Q,所以点Q的坐标为(-4,3).


科目:初中数学 来源: 题型:
【题目】一艘货轮往返于上下游两个码头之间,逆流而上需要6小时,顺流而下需要4小时,若船在静水中的速度为20千米/时,则水流的速度是_____千米/时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下面推理过程补充完整,在括号内注明理由:
已知:如图,BC//EF,AB=DE,BC=EF,试说明∠C=∠F;
解:∵BC//EF(已知)
∴∠ABC=∠__________ _________________________
在△ABC与△DEF中,
∵
∴△ABC≌△DEF _______
∴∠C=∠F ____________________________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),将两块直角三角尺的直角顶点C叠放在一起,

(1)若∠DCE=25°,∠ACB=;若∠ACB=150°,则∠DCE=;
(2)猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(3)如图(2),若是两个同样的直角三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小又有何关系,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC和△ADE均为等边三角形,连接BE,CD,点F,G,H分别为DE,BE,CD中点.
(1)当△ADE绕点A旋转时,如图1,则△FGH的形状为 ,说明理由;
(2)在△ADE旋转的过程中,当B,D,E三点共线时,如图2,若AB=3,AD=2,求线段FH的长;
(3)在△ADE旋转的过程中,若AB=a,AD=b(a>b>0),则△FGH的周长是否存在最大值和最小值,若存在,直接写出最大值和最小值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
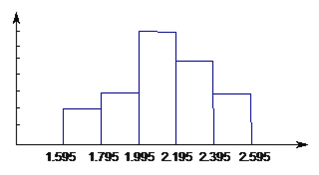
【题目】某校七年级学生进行体育测试,七年级(2)班男生的立定跳远成绩制成频数分布直方图,图中从左到右各矩形的高之比是![]() ,最后一组的频数是6,根据直方图所表达的信息,解答下列问题。
,最后一组的频数是6,根据直方图所表达的信息,解答下列问题。
(1)该班有多少名男生?
(2)若立定跳远的成绩在2.0米以上(包括2.0米)为合格率是多少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2008年5月30日,国务院关税税则委员会决定从当天起对纺织品出口关税作出进一步调整,对一些纺织品取消征收出口关税.在此背景下,某报报道了2008年1~4月份某市服装对外出口的情况,并绘制统计图如下:
请你根据统计图中提供的信息,回答下列问题:
(1)2008年1~4月份,该市服装企业出口额较多的是哪两个国家?
(2)2008年1~4月份,该市服装企业平均每月出口总额是多少万美元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】赵老师为了响应市政府“绿色出行”的号召,上下班由自驾车方式改为骑自行车方式.已知赵老师家距学校20千米,上下班高峰时段,自驾车的速度是自行车速度的2倍,骑自行车所用时间比自驾车所用时间多![]() 小时.求自驾车速度和自行车速度各是多少?
小时.求自驾车速度和自行车速度各是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com