
如图,点C在∠AOB的OB边上,用尺规作出了CN∥OA,作图痕迹中, 是( )
是( )

A.以点C为圆心,OD为半径的弧 B.以点C为圆心,DM为半径的弧
C.以点E为圆心,OD为半径的弧 D.以点E为圆心,DM为半径的弧
科目:初中数学 来源: 题型:
抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),B(3,0)两点,与y轴交于点C(0,﹣3).
(1)求该抛物线的解析式及顶点M的坐标;
(2)当y的值大于0时,求x的取值范围;
(3)分别求出△BCM与△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
数学课上,探讨角平分线的作法时,徐老师用直尺和圆规作角平分线,方法如下:
 作法:①如图①,在射线OA、OB上,分别截取OD、OE,使OD=OE;
作法:①如图①,在射线OA、OB上,分别截取OD、OE,使OD=OE;
②分别以点D和点E为圆心,适当长(大于线段DE长的一半)为半径作圆弧,在∠AOB的内部,两弧交于点C;
③作射线OC.
徐老师又介绍用角尺平分一个任意角的方法,作法如下:
如图②,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线.
(1)徐老师用尺规作图作角平分线时,用到的三角形全等的判定方法是__________;
(2)请证明徐老师用角尺平分一个任意角的 方法.
方法.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,有一长、宽、高分别为12cm,4cm,3cm的木箱,在它里面放一根细木条(木条的粗细忽略不计)要求木条不能露出木箱,请你算一算,能放入的细木条的最大长度是( )

A.13cm B.14cm C.15cm D.16cm
查看答案和解析>>
科目:初中数学 来源: 题型:
根据下列表格的对应值,判断方程ax2+bx+c=0(a≠0,a、b、c为常数)一个解的范围是( )
| x | 3.23 | 3.24 | 3.25 | 3.26 |
| ax2+bx+c | ﹣0.06 | ﹣0.02 | 0.03 | 0.09 |
A.3<x<3.23 B.3.23<x<3.24 C.3.24<x<3.25 D.3.25<x<3.26
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,点A,B的坐标分别是(-3,0),(0,6),动点P从点O出发,沿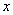 轴正方向以每秒1个单位的速度运动,同时动点
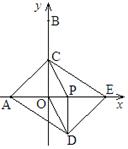
轴正方向以每秒1个单位的速度运动,同时动点 C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造□PCOD.在线段OP延长线上一动点E,且满足PE=AO.
C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造□PCOD.在线段OP延长线上一动点E,且满足PE=AO.
(1)当点C在线段OB上运动时,求证:四边形ADEC为平行四边形;
(2)当点P运动的时间为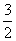 秒时,求此时四边形ADEC的周长是多少?
秒时,求此时四边形ADEC的周长是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com