Question

12．如图，已知函数y=x+1的图象与y轴交于点A，一次函数y=kx+b 的图象经过点B（0，-1），并且与x轴以及y=x+1的图象分别交于点C、D．
（1）若点D的横坐标为2，求直线BD的解析式和四边形AOCD的面积（即图中阴影部分的面积）；
（2）在第（1）小题的条件下，在x轴上是否存在这样的点P，使得以点P、A、D为顶点的三角形是等腰三角形？如果存在，求出点P坐标；如果不存在，说明理由．
（3）若y=kx+b与函数y=x+1的图象交于D始终在第三象限，则系数K的取值范围是-1＜k＜1且k≠0．（直接写结果）

Answer 1

分析 （1）先求出点D的坐标，再求出BD的解析式，然后根据S_{四边形AOCD}=S_△AOD+S_△COD即可求解；
（2）分三种情况讨论：①当DP=DA时，②当AP=DA时，③当PA=PD时；
（3）根据图象即可得出答案．

解答 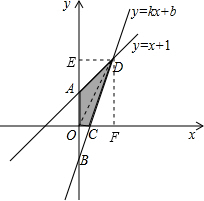解：（1）∵点D的横坐标为2，点D在y=x+1的图象上，
∴D（2，3），
∴$\left\{\begin{array}{l}{-1=b}\\{3=2k+b}\end{array}\right.$，
∴$\left\{\begin{array}{l}{k=2}\\{b=-1}\end{array}\right.$，
∴直线BD的解析式为y=2x-1，
∴A（0，1），C（$\frac{1}{2}$，0），
∴S_{四边形AOCD}=S_△AOD+S_△COD=$\frac{1}{2}$×1×2+$\frac{1}{2}$×$\frac{1}{2}$×3=$\frac{7}{4}$；
（2）存在；
∵D（2，3），
由y=x+1得到A（0，1），H（-1，0），
∴OA=OH，
∴∠HAO=∠QAD=45°，
∴AD=$\sqrt{2}$，
当AP=AD=2$\sqrt{2}$时，
在R_t△APO中，OP=$\sqrt{{AP}^{2}{-AO}^{2}}$=$\sqrt{7}$，
∴P（$\sqrt{7}$，0），（-$\sqrt{7}$，0）
当AP=DP时，点P在AD的中垂线上，
作AD的中垂线交x轴于P′，交y轴于Q，
∵∠QAD=45°，
∴∠QP′O=45°，
∴OP′=OQ=1+2，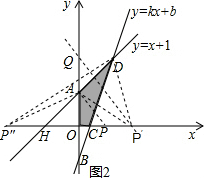
∴OP′（3，0），
当AD=PD=2$\sqrt{2}$＜3，
∴不存在，
综上所述；点P的坐标为：（$\sqrt{7}$，0），（-$\sqrt{7}$，0），（3，0）；

（3）若y=kx+b与函数y=x+1的图象交于D始终在第三象限，则-1＜k＜1且k≠0，
故答案为：-1＜k＜1且k≠0．

点评 本题考查了根据函数的解析式求点的坐标，待定系数法求一次函数的解析式，等腰直角三角形的性质，中垂线的性质，要注意的是（3）中，要根据P点的不同位置进行分类求解．