
【题目】如图,平面上有线段AB和点C,按下列语句要求画图与填空:
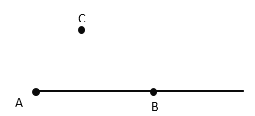
(1)作射线AC;
(2)用尺规在线段AB的延长线上截取BD=AC;
(3)连接BC
(4)有一只蚂蚁想从点A爬到点B,它应该沿路径(填序号)______(①AB,②![]() )爬行最近,这样爬行所运用到的数学原理是_____________________.
)爬行最近,这样爬行所运用到的数学原理是_____________________.
 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】已知:在一条东西向的双轨铁路上迎面驶来一快一慢两列火车,快车长![]() (单位长度)。慢车长
(单位长度)。慢车长![]() (单位长度),设正在行驶途中的某一时刻,如图,以两车之间的某点
(单位长度),设正在行驶途中的某一时刻,如图,以两车之间的某点![]() 为原点,取向右方向为正方向画数轴,此时快车
为原点,取向右方向为正方向画数轴,此时快车![]() 在数轴上表示的数是
在数轴上表示的数是![]() ,慢车头
,慢车头![]() 在数轴上表示的数是
在数轴上表示的数是![]() ,若快车
,若快车![]() 以
以![]() 个单位长度/秒的速度向右匀速继续行驶,同时慢车
个单位长度/秒的速度向右匀速继续行驶,同时慢车![]() 以
以![]() 个单位长度/秒的速度向左匀速继续行驶,且
个单位长度/秒的速度向左匀速继续行驶,且![]() 与
与![]() 互为相反数.
互为相反数.
(1)求此时刻快车头![]() 与慢车头
与慢车头![]() 之间相距多少单位长度?
之间相距多少单位长度?
(2)从此时刻开始算起,问再行驶多少秒两列火车行驶到车头![]() 、
、![]() 相距
相距![]() 个单位长度?
个单位长度?
(3)此时在快车![]() 上有一位爱到脑筋的七年级学生乘客
上有一位爱到脑筋的七年级学生乘客![]() ,他发现行驶中有一段时间,他的位置
,他发现行驶中有一段时间,他的位置![]() 到两列火车头
到两列火车头![]() 、
、![]() 的距离和加上到两列火车尾
的距离和加上到两列火车尾![]() 、
、![]() 的距离和是一个不变的值(即
的距离和是一个不变的值(即![]() 为定值),你认为学生
为定值),你认为学生![]() 发现的这一结论是否正确?若正确,求出增定值及所持续的时间;若不正确,请说明理由.
发现的这一结论是否正确?若正确,求出增定值及所持续的时间;若不正确,请说明理由.
![]()
附加题:
查看答案和解析>>
科目:初中数学 来源: 题型:
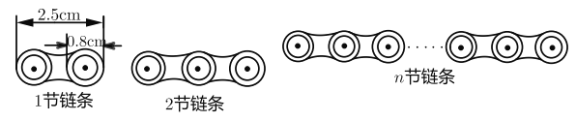
【题目】如图,自行车链条每节链条的长度为2.5cm ,交叉重叠部分的圆的直径为0.8cm.
(1)尝试: 2节链条总长度是________ ![]() , 3节链条总长度是________
, 3节链条总长度是________ ![]() .
.
(2)发现:用含![]() 的代数式表示
的代数式表示![]() 节链条总长度是________. ( 要求填写最简结果)
节链条总长度是________. ( 要求填写最简结果)
(3)应用:如果某种型号自行车链条总长度为![]() ,则它是由多少节这样的链条构成的?
,则它是由多少节这样的链条构成的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(小时),两车之间的距离为![]() (千米),图中的折线表示
(千米),图中的折线表示![]() 与
与![]() 的函数关系.
的函数关系.
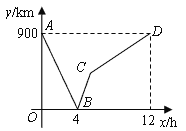
信息读取:
(1)甲、乙两地之间的距离为__________千米;
(2)请解释图中点![]() 的实际意义;
的实际意义;
图像理解:
(3)求慢车和快车的速度;
(4)求线段![]() 所示的
所示的![]() 与
与![]() 之间函数关系式.
之间函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AEAD=AHAF;其中结论正确的个数是( )
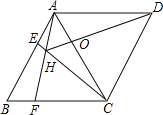
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
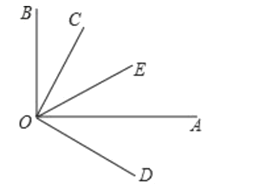
【题目】请补充完成以下解答过程,并在括号内填写该步骤的理由.已知:如图,![]() ,
,![]() ,OA平分
,OA平分![]() ,若
,若![]() ,求
,求![]() 的度数.
的度数.
解:因为![]() ,
,
所以![]() ________
________![]() .
.
因为_________![]() ,
,
所以![]() .
.
所以![]() .(__________________)
.(__________________)
因为![]() ,
,
所以![]() .
.
因为OA平分![]() ,
,
所以__________![]() _______°
_______°
所以![]() _______°.
_______°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,二次函数y=ax2+bx﹣4(a≠0)的图象与x轴交于A(﹣2,0)、C(8,0)两点,与y轴交于点B,其对称轴与x轴交于点D.
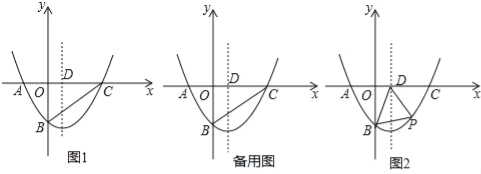
(1)求该二次函数的解析式;
(2)如图1,连结BC,在线段BC上是否存在点E,使得△CDE为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由;
(3)如图2,若点P(m,n)是该二次函数图象上的一个动点(其中m>0,n<0),连结PB,PD,BD,求△BDP面积的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将ABCD的AD边延长至点E,使DE=![]() AD,连接CE,F是BC边的中点,连接FD.
AD,连接CE,F是BC边的中点,连接FD.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=3,AD=4,∠A=60°,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.

(1)数轴上点A表示的数为________.
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数是多少?
②设点A的移动距离AA′=x.
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA′的中点,点E在线段OO′上,且OE=![]() OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com