
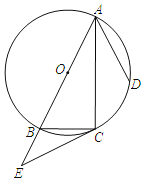
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,点D在⊙O上,AC平分∠BAD,延长AB到点E且有∠BCE=∠CAD.
(1)求证:CE是⊙O的切线;
(2)若AB=10,AD=6,求BC,CE的长.
【答案】(1)见解析;(2)![]() ,
,![]()
【解析】
(1)连接OC,根据等腰三角形的性质得到∠1=∠2,根据圆周角定理得到∠ACB=90°,根据角平分线的定义得到∠3=∠CAD,求得CE⊥OC,于是得到结论;
(2)连接CD,分别延长AD、BC相交于点F.根据三角形的内角得到∠3=∠CAD,根据相似三角形的性质得到![]() ,设BC=x,求得
,设BC=x,求得![]() ,根据相似三角形的性质即可得到结论.
,根据相似三角形的性质即可得到结论.
(1)证明:连接OC,
∵在⊙O中OB=OC,
∴∠1=∠2,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AC平分∠BAD,
∴∠3=∠CAD,
∵∠BCE=∠CAD,
∴∠3=∠CAD,
∴∠OCE=∠BCE+∠2=∠3+∠1=90°,
∴CE⊥OC,
∴CE是⊙O的切线;
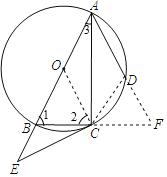
(2)解:连接CD,分别延长AD、BC相交于点F.
在Rt△ACB中,∠1=90°﹣∠3,
在Rt△ACF中,∠F=90°﹣∠CAD,
又∵∠3=∠CAD,
∴∠1=∠F,
∴在△ABF中,AB=AF,
∴BC=CF,
∵在⊙O中∠3=∠CAD,
∴BC=CD,
∴CD=CF,
∴在△CDF中,∠CDF=∠F,
∴∠1=∠CDF,
又∵∠F=∠F,
∴△CDF∽△ABF,
∴![]() ,
,
设BC=x,则有![]() ,
,
∴![]() ,
,
即![]() ,
,
在Rt△ACB中,![]() ,
,
∵在△BEC和△DAC中,∠BCE=∠CAD,∠EBC=∠ADC,
∴△BEC∽△DCA,
∴![]() ,
,
则![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】某天上午7:30,小芳在家通过滴滴打车软件打车前往动车站搭乘当天上午8:30的动车.记汽车的行驶时间为t小时,行驶速度为v千米/小时(汽车行驶速度不超过60千米/小时).根据经验,v,t的一组对应值如下表:
V(千米/小时) | 20 | 30 | 40 | 50 | 60 |
T(小时) | 0.6 | 0.4 | 0.3 | 0.25 | 0.2 |
(1)根据表中的数据描点,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)若小芳从开始打车到上车用了10分钟,小芳想在动车出发前半小时到达动车站,若汽车的平均速度为32千米/小时,小芳能否在预定的时间内到达动车站?请说明理由;
(3)若汽车到达动车站的行驶时间t满足0.3<t<0.5,求平均速度v的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
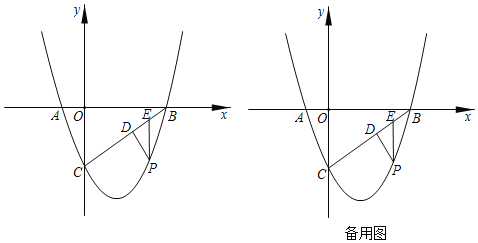
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于C点.
与x轴交于A、B两点,与y轴交于C点.
(1)点P是线段BC下方的抛物线上一点,过点P作PD⊥BC交BC于点D,过点P作EP∥y轴交BC于点E.点MN是直线BC上两个动点且MN=AO(xM<xN).当DE长度最大时,求PM+MN﹣![]() BN的最小值.
BN的最小值.
(2)将点A向左移动3个单位得点G,△GOC延直线BC平移运动得到三角形△G'O′C'(两三角形可重合),则在平面内是否存在点G',使得△G′BC为等腰三角形,若存在,直接写出满足条件的所有点G′的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:
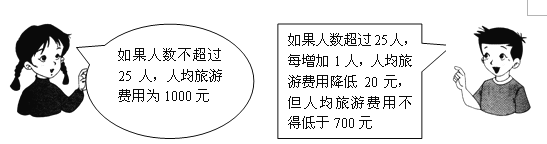 某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
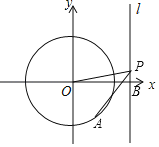
【题目】已知点A是圆心为坐标原点O且半径为3的圆上的动点,经过点B(4,0)作直线l⊥x轴,点P是直线l上的动点,若∠OPA=45°,则△BOP的面积的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
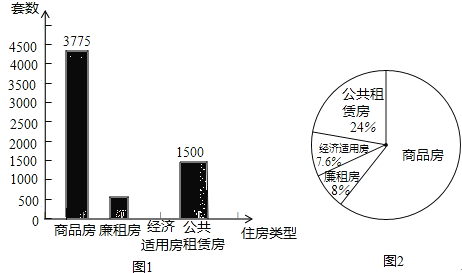
【题目】某市2012年国民经济和社会发展统计公报显示,2012年该市新开工的住房有商品房、廉租房、经济适用房和公共租赁房四种类型.老王对这四种新开工的住房套数和比例进行了统计,并将统计结果绘制成下面两幅统计图,请你结合图中所给信息解答下列问题:
(1)求经济适用房的套数,并补全图1;
(2)假如申请购买经济适用房的对象中共有950人符合购买条件,老王是其中之一.由于购买人数超过房子套数,购买者必须通过电脑摇号产生.如果对2012年新开工的经济适用房进行电脑摇号,那么老王被摇中的概率是多少?
(3)如果计划2014年新开工廉租房建设的套数要达到720套,那么2013~2014这两年新开工廉租房的套数的年平均增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
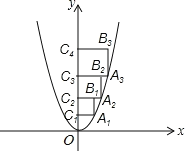
【题目】正方形A1B1C2C1,A2B2C3C2,A3B3C4C3按如图所示的方式放置,点A1、A2、A3和点C1、C2、C3、C4分别在抛物线y=x2和y轴上,若点C1(0,1),则正方形A3B3C4C3的面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
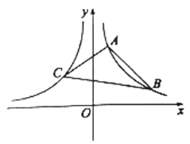
【题目】如图,已知反比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象关于
的图象关于![]() 轴对称,
轴对称,![]() ,
,![]() 是函数
是函数![]() 图象上的两点,连接
图象上的两点,连接![]() ,点
,点![]() 是函数
是函数![]() 图象上的一点,连接
图象上的一点,连接![]() ,
,![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 所在直线的表达式;
所在直线的表达式;
(3)求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com