
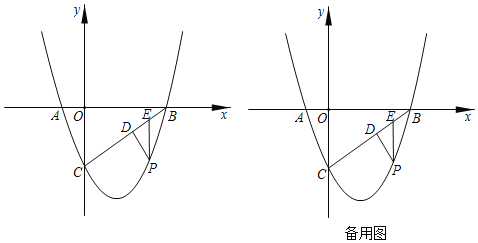
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于C点.
与x轴交于A、B两点,与y轴交于C点.
(1)点P是线段BC下方的抛物线上一点,过点P作PD⊥BC交BC于点D,过点P作EP∥y轴交BC于点E.点MN是直线BC上两个动点且MN=AO(xM<xN).当DE长度最大时,求PM+MN﹣![]() BN的最小值.
BN的最小值.
(2)将点A向左移动3个单位得点G,△GOC延直线BC平移运动得到三角形△G'O′C'(两三角形可重合),则在平面内是否存在点G',使得△G′BC为等腰三角形,若存在,直接写出满足条件的所有点G′的坐标,若不存在请说明理由.
【答案】(1)![]() ;(2)点G′(﹣4,0)或(﹣
;(2)点G′(﹣4,0)或(﹣![]() ,
,![]() ).
).
【解析】
(1)DE=PEsin∠EPD=![]() (
(![]() x﹣
x﹣![]() ﹣
﹣![]() x2+
x2+![]() x+
x+![]() ),当x=2时,DE最大,此时点P(2,﹣
),当x=2时,DE最大,此时点P(2,﹣![]() );MN=AO=1,将△BCO沿BC翻折得到△BCO′,将点P沿CB的方向平移1个单位得到点P′(
);MN=AO=1,将△BCO沿BC翻折得到△BCO′,将点P沿CB的方向平移1个单位得到点P′(![]() ,
,![]() ),作P′H⊥BO′交BO′于点H,交BC于点N,将点N沿BC方向平移1个单位得到点M,则点M、N为所求,即可求解;
),作P′H⊥BO′交BO′于点H,交BC于点N,将点N沿BC方向平移1个单位得到点M,则点M、N为所求,即可求解;
(2)分BC=BG′、BC=G′C、BG=CG′三种情况,分别求解即可.
(1)y=![]() =
=![]() (x﹣4)(x+1),
(x﹣4)(x+1),
故点A、B、C的坐标分别为:(﹣1,0)、(4,0)、(0,﹣![]() );
);
则直线BC的表达式为:y=![]() (x﹣4);
(x﹣4);
设点P(x,![]() ),则点E(x,
),则点E(x,![]() x﹣
x﹣![]() ),
),
∵![]() ,∠EPD=∠OBC,
,∠EPD=∠OBC,
∴DE=PEsin∠EPD=![]() (
(![]() x﹣
x﹣![]() ﹣
﹣![]() x2+
x2+![]() x+
x+![]() ),
),
当x=2时,DE最大,此时点P(2,﹣![]() );
);
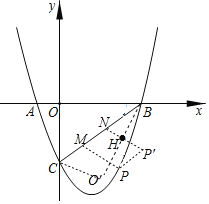
MN=AO=1,将△BCO沿BC翻折得到△BCO′,
将点P沿CB的方向平移1个单位得到点P′(![]() ,
,![]() ),作P′H⊥BO′交BO′于点H,交BC于点N,
),作P′H⊥BO′交BO′于点H,交BC于点N,
将点N沿BC方向平移1个单位得到点M,则点M、N为所求;
P′P∥MN,且PP′=MN,则四边形P′PNM为平行四边形,则P′N=PM,
∠CBO′=∠OBC=30°,则HN=NBsin30![]() =
=![]() BN,
BN,
PM+MN﹣![]() BN=MN+P′N﹣
BN=MN+P′N﹣![]() BN=MN+P′H为最小;
BN=MN+P′H为最小;
直线BO′的倾斜角为60°,则其表达式为:y=![]() (x﹣4)…①,
(x﹣4)…①,
则直线P′N表达式中的k为:﹣![]() ,其表达式为:y=﹣
,其表达式为:y=﹣![]() x+b,
x+b,
将点P′坐标代入并解得:
直线P′N的表达式为:y=﹣![]() x+
x+![]() …②,
…②,
联立①②并解得:x=![]() ,故点H(
,故点H(![]() ,
,![]() );
);
P′H=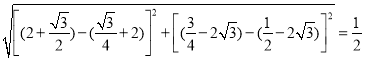 ,
,
PM+MN﹣![]() BN最小值=MN+P′N﹣
BN最小值=MN+P′N﹣![]() BN=MN+P′H=
BN=MN+P′H=![]() ;
;
(2)直线BC的表达式为:y=![]() (x﹣4);点G(﹣4,0),
(x﹣4);点G(﹣4,0),
设△GOC沿直线BC向上平移m个单位,则向右平移![]() m个单位,则点G′(m﹣4,
m个单位,则点G′(m﹣4,![]() m);
m);
BC2=![]() ,BG′2=(m﹣8)2+3m2,CG′2=(m﹣4)2+(
,BG′2=(m﹣8)2+3m2,CG′2=(m﹣4)2+(![]() m+
m+![]() )2=4m2+
)2=4m2+![]() ;
;
①当BC=BG′时,BC2=(m﹣8)2+3m2,方程无解;
②当BC=G′C时,同理可得:m=0;
③当BG=CG′时,同理可得:m=![]() ;
;
即m=0或![]() ,
,
故点G′(﹣4,0)或(﹣![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
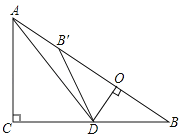
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在锐角![]() 中,边长
中,边长![]() 长为18,高
长为18,高![]() 长为12.
长为12.
(1)如图,矩形![]() 的边
的边![]() 在
在![]() 边上,其余两个顶点
边上,其余两个顶点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边上,
边上,![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的值.
的值.
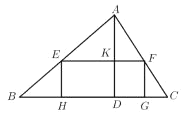
(2)设![]() ,矩形
,矩形![]() 的面积为
的面积为![]() ,求
,求![]() 于
于![]() 的函数关系式,并求
的函数关系式,并求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在某海域,一般指挥船在C处收到渔船在B处发出的求救信号,经确定,遇险抛锚的渔船所在的B处位于C处的南偏西45°方向上,且BC=60海里;指挥船搜索发现,在C处的南偏西60°方向上有一艘海监船A,恰好位于B处的正西方向.于是命令海监船A前往搜救,已知海监船A的航行速度为30海里/小时,问渔船在B处需要等待多长时间才能得到海监船A的救援?(参考数据:![]() ,
,![]() ,
,![]() 结果精确到0.1小时)
结果精确到0.1小时)

查看答案和解析>>
科目:初中数学 来源: 题型:
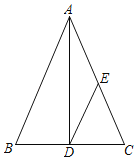
【题目】如图,在△ABC中,AB=AC,D是BC边的中点,连接AD,过点D作DE∥AB
(1)若∠C=70°,求∠BAD的度数;
(2)求证:AE=DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
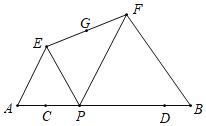
【题目】已知线段AB=12,C、D是AB上两点,且AC=DB=2,P是线段CD上一动点,在AB同侧分别作等边三角形APE和等边三角形PBF,G为线段EF的中点,点P由点C移动到点D时,G点移动的路径长度为_____
查看答案和解析>>
科目:初中数学 来源: 题型:
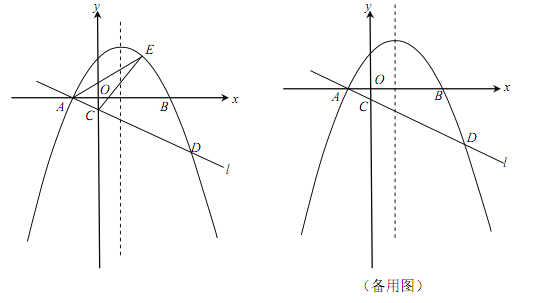
【题目】(本小题满分12分)如图,在平面直角坐标系xOy中,抛物线![]() (
(![]() )与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:
)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:![]() 与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
(1)直接写出点A的坐标,并求直线l的函数表达式(其中k,b用含a的式子表示);
(2)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为![]() ,求a的值;
,求a的值;
(3)设P是抛物线的对称轴上的一点,点Q在抛物线上,以点A,D,P,Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
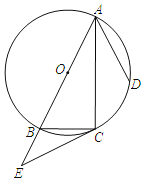
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,点D在⊙O上,AC平分∠BAD,延长AB到点E且有∠BCE=∠CAD.
(1)求证:CE是⊙O的切线;
(2)若AB=10,AD=6,求BC,CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com