
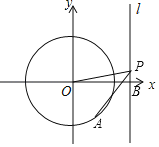
【题目】已知点A是圆心为坐标原点O且半径为3的圆上的动点,经过点B(4,0)作直线l⊥x轴,点P是直线l上的动点,若∠OPA=45°,则△BOP的面积的最大值为_____.
科目:初中数学 来源: 题型:
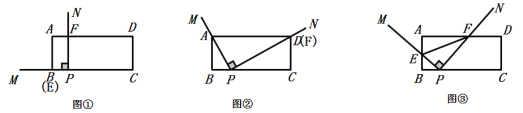
【题目】如图①,矩形![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 从
从![]() 处开始按顺时针方向旋转,
处开始按顺时针方向旋转,![]() 交边
交边![]() (或
(或![]() )于点
)于点![]() ,
,![]() 交边
交边![]() (或
(或![]() )于点
)于点![]() .当
.当![]() 旋转至
旋转至![]() 处时,
处时,![]() 的旋转随即停止.
的旋转随即停止.
(1)特殊情形:如图②,发现当![]() 过点
过点![]() 时,
时,![]() 也恰好过点
也恰好过点![]() ,此时
,此时![]() 是否与
是否与![]() 相似?并说明理由;
相似?并说明理由;
(2)类比探究:如图③,在旋转过程中,![]() 的值是否为定值?若是,请求出该定值;若不是,请说明理由;
的值是否为定值?若是,请求出该定值;若不是,请说明理由;
(3)拓展延伸:设![]() 时,
时,![]() 的面积为
的面积为![]() ,试用含
,试用含![]() 的代数式表示
的代数式表示![]() ;
;
①在旋转过程中,若![]() 时,求对应的
时,求对应的![]() 的面积;
的面积;
②在旋转过程中,当![]() 的面积为4.2时,求对应的
的面积为4.2时,求对应的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
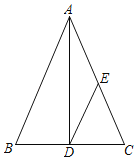
【题目】如图,在△ABC中,AB=AC,D是BC边的中点,连接AD,过点D作DE∥AB
(1)若∠C=70°,求∠BAD的度数;
(2)求证:AE=DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
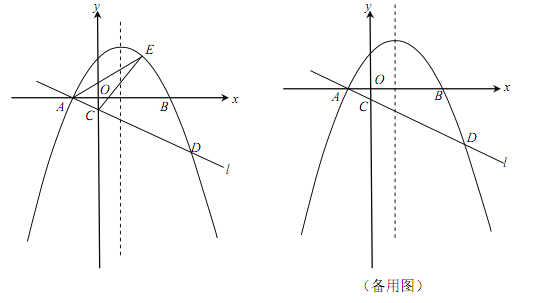
【题目】(本小题满分12分)如图,在平面直角坐标系xOy中,抛物线![]() (
(![]() )与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:
)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:![]() 与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
(1)直接写出点A的坐标,并求直线l的函数表达式(其中k,b用含a的式子表示);
(2)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为![]() ,求a的值;
,求a的值;
(3)设P是抛物线的对称轴上的一点,点Q在抛物线上,以点A,D,P,Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,sinA=![]() ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
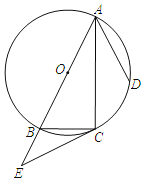
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,点D在⊙O上,AC平分∠BAD,延长AB到点E且有∠BCE=∠CAD.
(1)求证:CE是⊙O的切线;
(2)若AB=10,AD=6,求BC,CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三台县教育和体育局为帮助万福村李大爷“精准脱贫”,在网上销售李大爷自己手工做的竹帘,其成本为每张40元,当售价为每张80元时,每月可销售100张.为了吸引更多顾客,采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售5张.设每张竹帘的售价为![]() 元(
元(![]() 为正整数),每月的销售量为
为正整数),每月的销售量为![]() 张.
张.
(1)直接写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)设该网店每月获得的利润为![]() 元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
(3)李大爷深感扶贫政策给自己带来的好处,为了回报社会,他决定每月从利润中捐出200元资助贫困学生.为了保证捐款后每月利润不低于4220元,求销售单价应该定在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
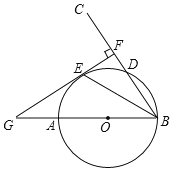
【题目】如图,AB是⊙O的直径,射线BC交⊙O于点D,E是劣弧AD上一点,且![]() =
=![]() ,过点E作EF⊥BC于点F,延长FE和BA的延长线交与点G.
,过点E作EF⊥BC于点F,延长FE和BA的延长线交与点G.
(1)证明:GF是⊙O的切线;
(2)若AG=6,GE=6![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两队参加了“端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程![]() (米)与时间
(米)与时间![]() (秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是( )
(秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是( )
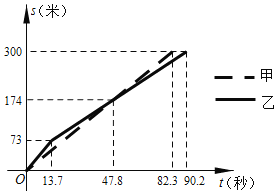
A. 乙队率先到达终点
B. 甲队比乙队多走了![]() 米
米
C. 在![]() 秒时,两队所走路程相等
秒时,两队所走路程相等
D. 从出发到![]() 秒的时间段内,乙队的速度慢
秒的时间段内,乙队的速度慢
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com