
【题目】如图1,在△ABC中,∠ABC=90°,BA=BC.将线段AB绕点A逆时针旋转90°得到线段AD,E是边BC上的一动点,连结DE交AC于点F,连结BF.
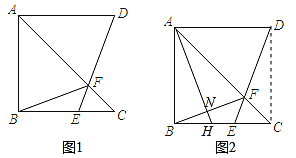
(1)求证:FB=FD;
(2)如图2,连结CD,点H在线段BE上(不含端点),且BH=CE,连结AH交BF于点N.
①判断AH与BF的位置关系,并证明你的结论;
②连接CN.若AB=2,请直接写出线段CN长度的最小值.
【答案】(1)见解析;(2)①AH⊥BF,见解析;②![]() .
.
【解析】
(1)证明△FAD≌△FAB(SAS)即可解决问题.
(2)①首先证明四边形ABCD是正方形,再证明∠BAH=∠CBF即可解决问题.
②如图3中,取AB的中点O,连接ON,OC.理由三角形的三边关系解决问题即可.
(1)证明:如图1中,

∵BA=BC,∠ABC=90°,
∴∠BAC=∠ACB=45°,
∵线段AB绕点A逆时针旋转90°得到线段AD,
∴∠BAD=90°,BA=AD,
∴∠FAD=∠FAB=45°,
∵AF=AF,
∴△FAD≌△FAB(SAS),
∴BF=DF.
(2)①解:结论:AH⊥BF.
理由:如图2中,连接CD.

∵∠ABC+∠BAD=180°,
∴AD∥BC,
∵AD=AB=BC,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴四边形ABCD是矩形,
∵AB=BC,
∴四边形ABCD是正方形,
∵BA=CD,∠ABH=∠DCE,BH=CE,
∴△ABH≌△DCE(SAS),
∴∠BAH=∠CDE,
∵∠FCD=∠FCB=45°,CF=CF,CD=CB,
∴△CFD≌△CFB(SAS),
∴∠CDF=∠CBF,
∴∠BAH=∠CBF,
∵∠CBF+∠ABF=90°,
∴∠BAH+∠ABF=90°,
∴∠ANB=90°,
∴AH⊥BF.
②如图3中,取AB的中点O,连接ON,OC.

∵∠ANB=90°,AO=OB,
∴ON=![]() AB=1,
AB=1,
在Rt△OBC中,OC=![]() ,
,
∵CN≥OC-ON,
∴CN≥![]() -1,
-1,
∴CN的最小值为![]() -1.
-1.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】某游乐场部分平面图如图所示,C,E,A在同一直线上,D,E,B在同一直线上,测得A处与E处的距离为80 m,C处与D处的距离为34 m,∠C=90°,∠ABE=90°,∠BAE=30°.( ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)
(1)求旋转木马E处到出口B处的距离;
(2)求海洋球D处到出口B处的距离(结果保留整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为12m,设AD的长为![]() m,DC的长为
m,DC的长为![]() m。
m。
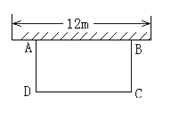
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)根据实际情况,对于(1)式中的函数自变量![]() 能否取值为4m,若能,求出
能否取值为4m,若能,求出![]() 的值,若不能,请说明理由;
的值,若不能,请说明理由;
(3)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
,![]()
(1)求抛物线的顶点坐标;
(2)若![]() ,
,
①求抛物线的解析式;
②)已知点![]() ,
,![]() ,将抛物线在
,将抛物线在![]() 的部分向上平移
的部分向上平移![]() 个单位得到图象
个单位得到图象![]() ,若图象
,若图象![]() 与线段
与线段![]() 恰有
恰有![]() 个公共点,结合函数的图象,直接写出
个公共点,结合函数的图象,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个判断:①当x>0时,y>0;②若a=-1,则b=3;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;④点C关于抛物线对称轴的对称点为E,点G、F分别在x轴和y轴上,当m=2时,四边形EDGF周长的最小值为![]() ,其中,判断正确的序号是( )
,其中,判断正确的序号是( )
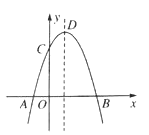
A.①②B.②③C.①③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB,AC是⊙O的弦,过点C作CE⊥AB于点D,交⊙O于点E,过点B作BF⊥AC于点F,交CE于点G,连接BE。

(1)求证:BE=BG;
(2)过点B作BH⊥AB交⊙O于点H,若BE的长等于半径,BH=4,AC=![]() ,求CE的长。
,求CE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班数学兴趣小组经过市场调查,整理出某种商品在第![]() 天的售价与销量的相关信息如下表:
天的售价与销量的相关信息如下表:
观察表格:根据表格解答下列问题:
| 0 | 1 | 2 |
| 1 | ||
| -3 | -3 |
(1)![]() __________.
__________.![]() _____________.
_____________.![]() ___________.
___________.
(2)在下图的直角坐标系中画出函数![]() 的图象,并根据图象,直接写出当
的图象,并根据图象,直接写出当![]() 取什么实数时,不等式
取什么实数时,不等式![]() 成立;
成立;

(3)该图象与![]() 轴两交点从左到右依次分别为
轴两交点从左到右依次分别为![]() 、
、![]() ,与
,与![]() 轴交点为
轴交点为![]() ,求过这三个点的外接圆的半径.
,求过这三个点的外接圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC的中点为O,点G,H在对角线AC上,AG=CH,直线GH绕点O逆时针旋转α角,与边AB、CD分别相交于点E、F(点E不与点A、B重合).
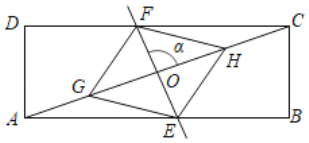
(1)求证:四边形EHFG是平行四边形;
(2)若∠α=90°,AB=9,AD=3,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 与x轴交于点B和点A(-1,0),与y轴交于点C,与一次函数
与x轴交于点B和点A(-1,0),与y轴交于点C,与一次函数![]() 交于点A和点D.
交于点A和点D.

1.求出![]() 的值;
的值;
2.若直线AD上方的抛物线存在点E,可使得△EAD面积最大,求点E的坐标;
3.点F为线段AD上的一个动点,点F到(2)中的点E的距离与到y轴的距离之和记为d,求d的最小值及此时点F的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com