
���� �ٽ����֪��֪��û�˵��ݵ�y��Ӧ��ס��2��3������y+1�㣬������¥¥�����ֱ�Ϊ��1��2������y����������ӳ�3���ɵó����ۣ�
�ڵ��ݵ�x��������ߵ���33-x�ˣ�������¥¥�����ֱ�Ϊ��1��2������33-x����������ӳ�3���ɵó����ۣ�
�۵��ݵ�x��������ߵ���x-1-y�ˣ�������¥¥�����ֱ�Ϊ��1��2������x-1-y����������ӳ�3���ɵó����ۣ�
�ܽ��٢ڢ۵ó�����������������ɵó����ۣ�
��� �⣺�ɳ�ʶ��֪��û�˵��ݵ�y��Ӧ�÷ֲ���2��3������y+1�㣮
�ʲ��˵���ֱ����¥�IJ������ܷ�Ϊ��3����1+2+3+��+y��=$\frac{3y��y+1��}{2}$��
���ݵ�x��������ߵ���33-x�ˣ���ÿ��סһ�ˣ�
�ʳ˵��ݵ�x����������߲������ܷ�Ϊ��3����1+2+��+33-x��=$\frac{3��33-x����34-x��}{2}$��
���ݵ�x��������ߵ���x-1-y�ˣ���y+1������ÿ��סһ�ˣ�
�ʳ˵��ݵ�x����������ߵ������ܷ�Ϊ��3����1+2+��+x-1-y��=$\frac{3��x-1-y����x-y��}{2}$��
�������ܷ�SΪ�٣��ڣ��۵ĺͣ�S=$\frac{3y��y+1��}{2}$+$\frac{3��33-x����34-x��}{2}$+$\frac{3��x-1-y����x-y��}{2}$=3x2+3y2-3xy-102x+3y+1683��
�ʴ�Ϊ����$\frac{3y��y+1��}{2}$����$\frac{3��33-x����34-x��}{2}$��$\frac{3��x-1-y����x-y��}{2}$��$\frac{3��x-1-y����x-y��}{2}$��
���� ���⿼������ı仯���ɣ�����Ĺؼ����ҳ�����1��2������n�ĺͣ����������е��⣬�ѶȲ��������������������ʧ�֣�������������λ��Ӽ��ɵó����ɣ��Ӷ��ó����ۣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
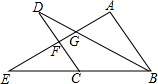 ��ͼ��AB��CD��AB=CD=BC����E��BC�ӳ�����һ�㣬����AE���ֱ�BD��CD�ڵ�G��F����AG=$\sqrt{5}$��GF=1����EF=4��
��ͼ��AB��CD��AB=CD=BC����E��BC�ӳ�����һ�㣬����AE���ֱ�BD��CD�ڵ�G��F����AG=$\sqrt{5}$��GF=1����EF=4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���߶�AB�ǰ뾶Ϊ6�ġ�O��ֱ������C�ǻ�AB���е㣬��M��N���߶�AB�ϣ�AM��BN����MN=5������MCN=45�㣬�߶�AM�ij���Ϊ3��4��
��ͼ���߶�AB�ǰ뾶Ϊ6�ġ�O��ֱ������C�ǻ�AB���е㣬��M��N���߶�AB�ϣ�AM��BN����MN=5������MCN=45�㣬�߶�AM�ij���Ϊ3��4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
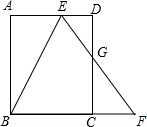 ��ͼ������ABCD�У�E��AD����һ�㣬F��BC�ӳ���һ�㣬EF��CD�ڵ�G������BE����BEƽ�֡�AEF��G��CD�ߵ��е㣬tan��ABE=$\frac{1}{2}$����$\frac{DE}{AE}$��ֵΪ$\frac{3}{4}$��
��ͼ������ABCD�У�E��AD����һ�㣬F��BC�ӳ���һ�㣬EF��CD�ڵ�G������BE����BEƽ�֡�AEF��G��CD�ߵ��е㣬tan��ABE=$\frac{1}{2}$����$\frac{DE}{AE}$��ֵΪ$\frac{3}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
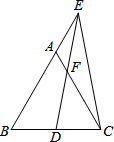 ��ͼ���ڵȱߡ�ABC�У���D��BC�е㣬��E��BA���ӳ����ϣ�ED=EC��AC��ED���ڵ�F����AE=$\frac{12}{5}$����CF=$\frac{18}{5}$��
��ͼ���ڵȱߡ�ABC�У���D��BC�е㣬��E��BA���ӳ����ϣ�ED=EC��AC��ED���ڵ�F����AE=$\frac{12}{5}$����CF=$\frac{18}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com