
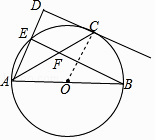
【题目】如图,点E在以AB为直径的⊙O上,点C是 ![]() 的中点,过点C作CD垂直于AE,交AE的延长线于点D,连接BE交AC于点F.
的中点,过点C作CD垂直于AE,交AE的延长线于点D,连接BE交AC于点F. 
(1)求证:CD是⊙O的切线;
(2)若cos∠CAD= ![]() ,BF=15,求AC的长.
,BF=15,求AC的长.
【答案】
(1)证明:连接OC,如图1所示.
∵点C是 ![]() 的中点,
的中点,
∴ ![]() =
= ![]() ,
,
∴OC⊥BE.
∵AB是⊙O的直径,
∴AD⊥BE,
∴AD∥OC.
∵AD⊥CD,
∴OC⊥CD,
∴CD是⊙O的切线.
(2)解:过点O作OM⊥AC于点M,如图2所示.

∵点C是 ![]() 的中点,
的中点,
∴ ![]() =
= ![]() ,∠BAC=∠CAE,
,∠BAC=∠CAE,
∴ ![]() =
= ![]() .
.
∵cos∠CAD= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AB= ![]() BF=20.
BF=20.
在Rt△AOM中,∠AMO=90°,AO= ![]() AB=10,cos∠OAM=cos∠CAD=
AB=10,cos∠OAM=cos∠CAD= ![]() ,
,
∴AM=AOcos∠OAM=8,
∴AC=2AM=16.
【解析】(1)连接OC,由点C是 ![]() 的中点利用垂径定理可得出OC⊥BE,由AB是⊙O的直径可得出AD⊥BE,进而可得出AD∥OC,再根据AD⊥CD可得出OC⊥CD,由此即可证出CD是⊙O的切线.(2)过点O作OM⊥AC于点M,由点C是
的中点利用垂径定理可得出OC⊥BE,由AB是⊙O的直径可得出AD⊥BE,进而可得出AD∥OC,再根据AD⊥CD可得出OC⊥CD,由此即可证出CD是⊙O的切线.(2)过点O作OM⊥AC于点M,由点C是 ![]() 的中点利用圆周角定理可得出∠BAC=∠CAE,根据角平分线的定理结合cos∠CAD=
的中点利用圆周角定理可得出∠BAC=∠CAE,根据角平分线的定理结合cos∠CAD= ![]() 可求出AB的长度,在Rt△AOM中,通过解直角三角形可求出AM的长度,再根据垂径定理即可得出AC的长度.
可求出AB的长度,在Rt△AOM中,通过解直角三角形可求出AM的长度,再根据垂径定理即可得出AC的长度.
【考点精析】本题主要考查了解直角三角形的相关知识点,需要掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,AB∥DC,连接BD,BE平分∠ABD,BE⊥AD,∠EBC和∠DCB的角平分线相交于点F,若∠ADC=110°,则∠F的度数为( )
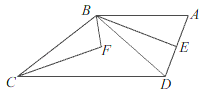
A. 115° B. 110° C. 105° D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两个工程队共同修建一条公路,从两端同时开始,到工程结束时,甲工程 队共施工了![]() 天,乙队在中途接到紧急任务停止施工一段时间,回来后按照以前的施工 速度继续施工至结束,设甲、乙两工程队各自施工的长度分別为
天,乙队在中途接到紧急任务停止施工一段时间,回来后按照以前的施工 速度继续施工至结束,设甲、乙两工程队各自施工的长度分別为![]() (米),
(米),![]() (米),甲 队施工的时间为
(米),甲 队施工的时间为![]() (天),
(天),![]() ,
,![]() 与
与![]() 之间的函数图象如图所示.
之间的函数图象如图所示.
(1)这条公路的总长度是______米;
(2)求乙队在恢复施工后,![]() 与
与![]() 之间的函数表 达式;
之间的函数表 达式;
(3)求在修建该条公路的过程中,甲、乙两队共同修建完![]() 米长时甲队施工的天数.
米长时甲队施工的天数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与坐标轴分别交于
与坐标轴分别交于![]() ,
,![]() 两点,以线段
两点,以线段![]() 为边,在第一象限内作正方形
为边,在第一象限内作正方形![]() ,将正方形
,将正方形![]() 沿
沿![]() 轴负方向,平移
轴负方向,平移![]() 个单位长度,使点
个单位长度,使点![]() 恰好落在直线
恰好落在直线![]() 上,则
上,则![]() 的值为________.
的值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB交CB于F.
(1)CD与EF平行吗?并说明理由;
(2)若∠A=72°,求∠FEC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图△ABC的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),如将B点向右平移2个单位后再向上平移4个单位到达B1点,若设△ABC的面积为S1 , △AB1C的面积为S2 , 则S1 , S2的大小关系为( )
A.S1>S2
B.S1=S2
C.S1<S2
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为解决部分市民冬季集中取暖问题需铺设一条长3000米的管道,为尽量减少施工对交通造成的影响,实施施工时“…”,设实际每天铺设管道x米,则可得方程 ![]() ,根据此情景,题中用“…”表示的缺失的条件应补为( )
,根据此情景,题中用“…”表示的缺失的条件应补为( )
A.每天比原计划多铺设10米,结果延期15天才完成
B.每天比原计划少铺设10米,结果延期15天才完成
C.每天比原计划多铺设10米,结果提前15天才完成
D.每天比原计划少铺设10米,结果提前15天才完成
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,三个半圆依次相外切,它们的圆心都在x轴的正半轴上并与直线y=![]() x相切,设半圆C1、半圆C2、半圆C3的半径分别是r1、r2、r3 , 则当r1=1时,r3= .
x相切,设半圆C1、半圆C2、半圆C3的半径分别是r1、r2、r3 , 则当r1=1时,r3= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com