
【题目】如图,某位老师在讲“实数”时,画了一个图,即“以数轴的单位长线段为边作一个正方形,然后以原点为圆心,正方形的对角线长为半径画弧交数轴于一点![]() ”,作这样的图用来说明:
”,作这样的图用来说明:
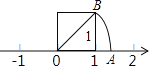
作图:请你在数轴上找出![]() 对应的点.
对应的点.
 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象的一支在平面直角坐标系中的位置如图所示,根据图象回答下列问题:
的图象的一支在平面直角坐标系中的位置如图所示,根据图象回答下列问题:
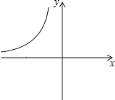
(1)图象的另一支在第________象限;在每个象限内,![]() 随
随![]() 的增大而________;
的增大而________;
(2)常数![]() 的取值范围是________;
的取值范围是________;
(3)若此反比例函数的图象经过点![]() ,求
,求![]() 的值.点
的值.点![]() 是否在这个函数图象上?点
是否在这个函数图象上?点![]() 呢?
呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=6,BC=8,动点P从A点出发,以1cm/s的速度,沿A—C—B向B点运动,同时,动点Q从C点出发,以2cm/s的速度,沿C—B—A向A点运动,当其中一点运动到终点时,两点同时停止运动。设运动时间为t秒,当t=_______秒时,△PCQ的面积等于8cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,老师提出问题:如图,有一张长4dm,宽3dm的长方形纸板,在纸板的四个角裁去四个相同的小正方形,然后把四边折起来,做成一个无盖的盒子,问小正方形的边长为多少时,盒子的体积最大.

下面是探究过程,请补充完整:
(1)设小正方形的边长为x dm,体积为y dm3,根据长方体的体积公式得到y和x的关系式: ;
(2)确定自变量x的取值范围是 ;
(3)列出y与x的几组对应值.
x/dm | … |
|
|
|
|
|
|
|
|
|
| … |
y/dm3 | … | 1.3 | 2.2 | 2.7 | m | 3.0 | 2.8 | 2.5 | n | 1.5 | 0.9 | … |
(4)在下面的平面直角坐标系![]() 中,描出补全后的表中各对对应值为坐标的点,并画出该函数的图象如下图;
中,描出补全后的表中各对对应值为坐标的点,并画出该函数的图象如下图;
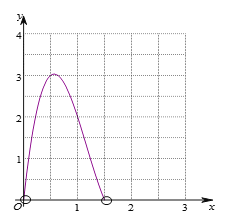
结合画出的函数图象,解决问题:
当小正方形的边长约为 dm时,(保留1位小数),盒子的体积最大,最大值约为 dm3.(保留1位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,三角形ABC的三个顶点都在正方形方格的格点上
(1)写出A、B、C三点的坐标;
(2)若△ABC各顶点的横坐标不变,纵坐标都乘以-1,请你再坐标系中描出对应的点A′、B′、C′,并依次连接这三个点,则所得的△A′B′C′与原△ABC有怎样的位置关系?
(3)在(2)的基础上,纵坐标都不变,横坐标都乘以-1,在同一坐标系中描出对应的点A″、B″、C″,并依次连接这三个点,所得的△A″B″C″与原△ABC有怎样的位置关系?
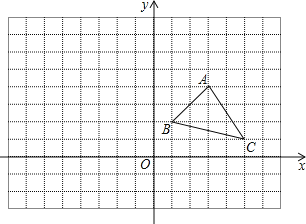
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )

A.带①去B.带②去C.带③去D.带①和②去
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,∠D=∠B=90°.
(1)填空:∠DAB+∠BCD= °;
(2)若AE平分∠DAB,CF平分∠BCD,求证:AE∥CF.
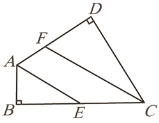
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,边长为1的正方形网格中,![]() 的三个顶点
的三个顶点![]() 、
、![]() 、
、![]() 都在格点上.
都在格点上.
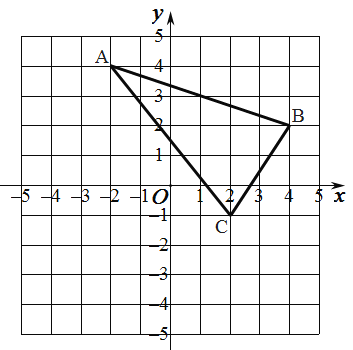
(1)作关于![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ,(其中
,(其中![]() 、
、![]() 、
、![]() 的对称点分别是
的对称点分别是![]() 、
、![]() 、
、![]() ),并写出点
),并写出点![]() 坐标;
坐标;
(2)![]() 为
为![]() 轴上一点,请在图中画出使
轴上一点,请在图中画出使![]() 的周长最小时的点
的周长最小时的点![]() (不写画法,保留画图痕迹),并直接写出点
(不写画法,保留画图痕迹),并直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售樱桃,已知樱桃的进价为15元/千克,如果售价为20元/千克,那么每天可售出250千克,如果售价为25元/千克,那么每天可售出200千克,经调查发现:每天的销售量y(千克)与售价x(元/千克)之间 存在一次函数关系.
(1)求y与x之间的函数关系式;
(2)若该超市每天要获得利润810元,同时又要让消费者得到实惠,则售价x应定于多少元?
(3)若樱桃的售价不得高于28元/千克,请问售价定为多少时,该超市每天销售樱桃所获的利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com