
如图,A(0,1),M(3,2),N(4,4).动点 P 从点 A 出发,沿 y 轴以每秒 1 个单位长的速 度向上移动,且过点 P 的直线 l:y=﹣x+b 也随之移动,设移动时间为 t 秒.若点 M,N 位于直线 l 的异侧,则 t 的取值范围是 .
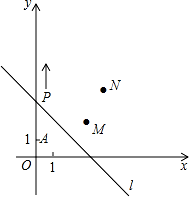
4<t<7
【考点】一次函数图象与几何变换.
【专题】计算题.
【分析】分别求出直线 l 经过点 M、点 N 时的 t 值,即可得到 t 的取值范围.
【解答】解:当直线 y=﹣x+b 过点 M(3,2)时, 2=﹣3+b,
解得:b=5,
5=1+t, 解得 t=4.
当直线 y=﹣x+b 过点 N(4,4)时, 4=﹣4+b,
解得:b=8,
8=1+t, 解得 t=7.
故若点 M,N 位于 l 的异侧,t 的取值范围是:4<t<7. 故答案为:4<t<7.
【点评】本题考查了坐标平面内一次函数的图象与性质,得出直线 l 经过点 M、点 N 时的 t 值是解 题关键.


科目:初中数学 来源: 题型:
△ABC 三个顶点的坐标分别为 A(1,1),B(4,2),C(3,4).
(1)请画出△ABC 向左平移 5 个单位长度后得到的△A1B1C1;
在 x 轴上求作一点 P,使△PAB 的周长最小,请画出△PAB,并直接写出 P 的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
下列 6 个实数中:①3.14;②﹣0.102030405…;③0.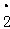 ;④ ;⑤ ;⑥ð.其中无理数的 个数共有( )
;④ ;⑤ ;⑥ð.其中无理数的 个数共有( )
A.2 个 B.3 个 C.4 个 D.5 个
查看答案和解析>>
科目:初中数学 来源: 题型:
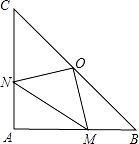
如图,在△ABC 中,∠A=90°,AB=AC,O 是 BC 的中点,如果在 AB 和 AC 上分别有一个动 点 M、N 在移动,且在移动时保持 AN=BM.
(1)请你判断△OMN 的形状,并说明理由. 若 BC=2 ,则 MN 的最小值为 .
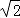
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com