
°æƒø°ø“—÷™£¨»ÁÕº£¨≈◊ŒÔœþy£Ωax2£´bx£´c (a°Ÿ0)µƒ∂•µ„Œ™M (1£¨9), æ≠π˝≈◊ŒÔœþ…œµƒ¡Ωµ„A(£≠3£¨£≠7)∫ÕB (3, m)µƒ÷±œþΩª≈◊ŒÔœþµƒ∂‘≥∆÷·”⁄µ„C£Æ

(1)«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω∫Õ÷±œþABµƒΩ‚Œˆ Ω£ª
(2)‘⁄≈◊ŒÔœþ…œ «∑ҥʑ⁄µ„D£¨ πµ√S°˜DAC£Ω2S°˜DCM?»Ù¥Ê‘⁄£¨«Û≥ˆµ„Dµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
(3)»Ùµ„P‘⁄≈◊ŒÔœþ…œ£¨µ„Q‘⁄x÷·…œ£¨µ±“‘µ„A°¢M°¢P°¢QŒ™∂•µ„µƒÀƒ±þ–Œ «∆Ω––Àƒ±þ–Œ ±£¨÷±Ω”–¥≥ˆ¬˙◊„◊„Ãıº˛µƒµ„Pµƒ◊¯±Í£Æ
°æ¥∞∏°ø£®1£©≈◊ŒÔœþµƒ±Ì¥Ô ΩŒ™£∫![]() £¨÷±œþ
£¨÷±œþ![]() µƒ±Ì¥Ô ΩŒ™£∫
µƒ±Ì¥Ô ΩŒ™£∫![]() £ª£®2£©µ„D
£ª£®2£©µ„D![]() ªÚ
ªÚ![]() £ª£®3£©µ„
£ª£®3£©µ„![]() ªÚ
ªÚ![]() ªÚ
ªÚ![]() £¨
£¨![]() ªÚ
ªÚ![]() £¨
£¨![]() £Æ
£Æ
°æΩ‚Œˆ°ø
£®1£©…Ë∂˛¥Œ∫Ø ˝±Ì¥Ô ΩŒ™£∫![]() £¨¿˚”√∂•µ„ Ωº¥ø…«ÛΩ‚£ª
£¨¿˚”√∂•µ„ Ωº¥ø…«ÛΩ‚£ª
£®2£©»ÁÕº£¨…˵„![]() £¨µ„
£¨µ„![]() £¨±Ì æ≥ˆDH£¨MC≥§∂»£¨∏˘æð
£¨±Ì æ≥ˆDH£¨MC≥§∂»£¨∏˘æð![]() £¨¡–∑Ω≥ëÛΩ‚º¥ø…£ª
£¨¡–∑Ω≥ëÛΩ‚º¥ø…£ª
£®3£©∑÷![]() «∆Ω––Àƒ±þ–Œµƒ“ªÃı±þ°¢
«∆Ω––Àƒ±þ–Œµƒ“ªÃı±þ°¢![]() «∆Ω––Àƒ±þ–Œµƒ∂‘Ω«œþ¡Ω÷÷«Èøˆ£¨∑÷±«ÛΩ‚º¥ø…£Æ
«∆Ω––Àƒ±þ–Œµƒ∂‘Ω«œþ¡Ω÷÷«Èøˆ£¨∑÷±«ÛΩ‚º¥ø…£Æ
Ω‚£∫£®1£©°þ≈◊ŒÔœþy£Ωax2£´bx£´c (a°Ÿ0)µƒ∂•µ„Œ™M (1£¨9)£¨
°ý…Ë∂˛¥Œ∫Ø ˝Ω‚Œˆ ΩŒ™£∫![]() £¨
£¨
°þA(£≠3£¨£≠7)‘⁄≈◊ŒÔœþ…œ£¨
°ý![]() £¨
£¨
Ω‚µ√£∫![]() £¨
£¨
π ≈◊ŒÔœþµƒ±Ì¥Ô ΩŒ™£∫![]() £¨
£¨
°þB (3, m)‘⁄≈◊ŒÔœþ…œ£¨
À˘“‘![]()
°ýµ„Bµƒ◊¯±ÍŒ™![]() £¨
£¨
…Ë÷±œþABΩ‚Œˆ ΩŒ™![]() £¨
£¨
°ý![]() £¨
£¨
Ω‚µ√![]() £¨
£¨
°ý÷±œþ![]() µƒ±Ì¥Ô ΩŒ™£∫
µƒ±Ì¥Ô ΩŒ™£∫![]() £ª
£ª
£®2£©¥Ê‘⁄£¨¿Ì”…£∫
”…∂˛¥Œ∫Ø ˝![]() µ√∂‘≥∆÷·Œ™£∫
µ√∂‘≥∆÷·Œ™£∫![]() £¨‘Úµ„
£¨‘Úµ„![]() £¨
£¨
π˝µ„![]() ◊˜
◊˜![]() ÷·µƒ∆Ω––œþΩª
÷·µƒ∆Ω––œþΩª![]() ”⁄µ„
”⁄µ„![]() £¨
£¨

…˵„![]() £¨µ„
£¨µ„![]() £¨
£¨
°ýDH=![]() £¨MC=9-1=8£¨
£¨MC=9-1=8£¨
![]() £¨
£¨
‘Ú![]() £¨
£¨
Ω‚µ√£∫![]() ªÚ5£¨
ªÚ5£¨
𠵄D![]() ªÚ
ªÚ![]() £ª
£ª
£®3£©…˵„![]() °¢µ„
°¢µ„![]() £¨
£¨![]() £¨
£¨
¢Ÿµ±![]() «∆Ω––Àƒ±þ–Œµƒ“ªÃı±þ ±£¨
«∆Ω––Àƒ±þ–Œµƒ“ªÃı±þ ±£¨
µ„![]() œÚ◊Û∆Ω“∆4∏ˆµ•ŒªœÚœ¬∆Ω“∆16∏ˆµ•Œªµ√µΩ
œÚ◊Û∆Ω“∆4∏ˆµ•ŒªœÚœ¬∆Ω“∆16∏ˆµ•Œªµ√µΩ![]() £¨
£¨
°ýµ„![]() œÚ◊Û∆Ω“∆4∏ˆµ•ŒªœÚœ¬∆Ω“∆16∏ˆµ•Œªµ√µΩµ„
œÚ◊Û∆Ω“∆4∏ˆµ•ŒªœÚœ¬∆Ω“∆16∏ˆµ•Œªµ√µΩµ„![]() £¨
£¨
°ýt=-16,
‘Ú![]() £¨
£¨
Ω‚µ√£∫![]() ªÚ
ªÚ![]() £¨
£¨
𠵄![]() ªÚ
ªÚ![]() £ª
£ª
¢⁄µ±![]() «∆Ω––Àƒ±þ–Œµƒ∂‘Ω«œþ ±£¨
«∆Ω––Àƒ±þ–Œµƒ∂‘Ω«œþ ±£¨
”…÷–µ„π´ Ωµ√£∫![]() £¨
£¨![]() £¨
£¨
°þ![]() £¨
£¨
°ý![]()
Ω‚µ√£∫![]() £¨
£¨
𠵄![]() £¨
£¨![]() ªÚ
ªÚ![]() £¨
£¨![]() £ª
£ª
◊€…œ£¨µ„![]() ªÚ
ªÚ![]() ªÚ
ªÚ![]() £¨
£¨![]() ªÚ
ªÚ![]() £¨
£¨![]() £Æ
£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øπÿ”⁄xµƒ∑Ω≥ã∫2£®x©Åk£©£Ωx©Å4¢Ÿ∫Õπÿ”⁄xµƒ“ª‘™∂˛¥Œ∑Ω≥ã∫£®k©Å1£©x2+2mx+£®3©Åk£©+n£Ω0¢⁄£®k°¢m°¢næ˘Œ™ µ ˝£©£¨∑Ω≥⟵ƒΩ‚Œ™∑«’˝ ˝£Æ
£®1£©«Ûkµƒ»°÷µ∑∂Œß£ª
£®2£©»Áπ˚∑Ω≥â⁄µƒΩ‚Œ™∏∫’˚ ˝£¨k©Åm£Ω2£¨2k©Ån£Ω6«“kŒ™’˚ ˝£¨«Û’˚ ˝mµƒ÷µ£ª
£®3£©µ±∑Ω≥â⁄”–¡Ω∏ˆ µ ˝∏˘x1°¢x2£¨¬˙◊„£®x1+x2£©£®x1©Åx2£©+2m£®x1©Åx2+m£©£Ωn+5£¨«“kŒ™’˝’˚ ˝£¨ ‘≈–∂œ|m|°Ð2 «∑Ò≥…¡¢£ø«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
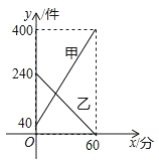
°æƒø°øƒ≥øϵðπ´Àæ√øÃÏ…œŒÁ9£∫00£≠10£∫00Œ™ºØ÷–¿øº˛∫Õ≈…º˛ ±∂Œ£¨º◊≤÷ø‚”√¿¥¿ø ’øϺ˛£¨““≤÷ø‚”√¿¥≈…∑¢øϺ˛£¨∏√ ±∂Œƒ⁄º◊°¢““¡Ω≤÷ø‚µƒøϺ˛ ˝¡øy£®º˛£©”Î ±º‰x£®∑÷£©÷ƺ‰µƒ∫Ø ˝ÕºœÛ»ÁÕºÀ˘ 棨ƒ«√¥µ±¡Ω≤÷ø‚øÏµðº˛ ˝œýÕ¨ ±£¨¥Àøõƒ ±º‰Œ™__________£ª
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∏ßÀ≥ –ƒ≥–£œÎ÷™µ¿—ß…˙∂‘°∞“£‘∂µƒ∫’Õº∞¢¿≠°±£¨°∞∆Ï≈€π ¿Ô°±µ»º“œÁ¬√”Œ∆∑≈∆µƒ¡ÀΩ‚≥Ã∂»£¨Àʪ˙≥È»°¡À≤ø∑÷—ß…˙Ω¯––Œ æ̵˜≤È£¨Œ æÌ”–Àƒ∏ˆ—°œÓ£®√øŒª±ªµ˜≤ȵƒ—ß…˙±ÿ—°«“÷ª—°“ªœÓ£©A£Æ Æ∑÷¡ÀΩ‚£¨B£Æ¡ÀΩ‚Ωœ∂ý£¨C£Æ¡ÀΩ‚Ωœ…Ÿ£¨D£Æ≤ª÷™µ¿£ÆΩ´µ˜≤ȵƒΩ·π˚ªÊ÷∆≥…»Áœ¬¡Ω∑˘≤ªÕÍ’˚µƒÕ≥º∆Õº£¨«Î∏˘æð¡Ω∑˘Õ≥º∆Õº÷–µƒ–≈œ¢ªÿ¥œ¬¡–Œ £∫
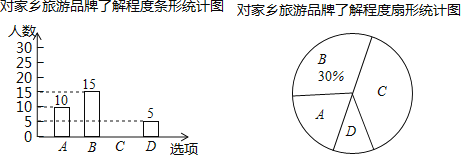
£®1£©±æ¥Œµ˜≤È¡À∂ý…Ÿ√˚—ß…˙£ø
£®2£©≤π»´Ãı–ŒÕ≥º∆Õº£ª
£®3£©∏√–£π≤”–500√˚—ß…˙£¨«Îƒ„π¿º∆°∞ Æ∑÷¡ÀΩ‚°±µƒ—ß…˙”–∂ý…Ÿ√˚£ø
£®4£©‘⁄±ªµ˜≤È°∞ Æ∑÷¡ÀΩ‚°±µƒ—ß…˙÷–”–Àƒ√˚—ß…˙ª·∏…≤ø£¨À˚√«÷–”–3√˚ƒ–…˙∫Õ1√˚≈Æ…˙£¨—ß–£œÎ¥”’‚4»À÷–»Œ—°¡Ω»À◊ˆº“œÁ¬√”Œ∆∑≈∆–˚¥´‘±£¨«Î”√¡–±ÌªÚª≠ ˜◊¥Õº∑®«Û≥ˆ±ª—°÷–µƒ¡Ω»À«°∫√ «“ªƒ–“ª≈Ƶƒ∏≈¬ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™Ω´≈◊ŒÔœþ![]() —ÿ
—ÿ![]() ÷·œÚ…œ∑≠’€”ÎÀ˘µ√≈◊ŒÔœþŒß≥…“ª∏ˆ∑‚±’«¯”Ú£®∞¸¿®±þΩÁ£©£¨‘⁄’‚∏ˆ«¯”Úƒ⁄”–5∏ˆ’˚µ„£®µ„
÷·œÚ…œ∑≠’€”ÎÀ˘µ√≈◊ŒÔœþŒß≥…“ª∏ˆ∑‚±’«¯”Ú£®∞¸¿®±þΩÁ£©£¨‘⁄’‚∏ˆ«¯”Úƒ⁄”–5∏ˆ’˚µ„£®µ„![]() ¬˙◊„∫·°¢◊ð◊¯±Í∂ºŒ™’˚ ˝£¨‘Ú∞—µ„
¬˙◊„∫·°¢◊ð◊¯±Í∂ºŒ™’˚ ˝£¨‘Ú∞—µ„![]() Ω–◊ˆ°∞’˚µ„°±£©.œ÷Ω´≈◊ŒÔœþ
Ω–◊ˆ°∞’˚µ„°±£©.œ÷Ω´≈◊ŒÔœþ![]() —ÿ
—ÿ![]() ÷·œÚœ¬∑≠’€£¨À˘µ√≈◊ŒÔœþ”Α≠≈◊ŒÔœþÀ˘Œß≥…µƒ∑‚±’«¯”Úƒ⁄£®∞¸¿®±þΩÁ£©«°”–11∏ˆ’˚µ„£¨‘Ú
÷·œÚœ¬∑≠’€£¨À˘µ√≈◊ŒÔœþ”Α≠≈◊ŒÔœþÀ˘Œß≥…µƒ∑‚±’«¯”Úƒ⁄£®∞¸¿®±þΩÁ£©«°”–11∏ˆ’˚µ„£¨‘Ú![]() µƒ»°÷µ∑∂Œß «£® £©
µƒ»°÷µ∑∂Œß «£® £©

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄¡‚–Œ![]() ÷–£¨
÷–£¨![]() ∑÷±Œ™±þ
∑÷±Œ™±þ![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() …œµƒµ„£®≤ª”Î∂Àµ„÷ÿ∫œ£©£Æ∂‘”⁄»Œ“‚¡‚–Œ
…œµƒµ„£®≤ª”Î∂Àµ„÷ÿ∫œ£©£Æ∂‘”⁄»Œ“‚¡‚–Œ![]() £¨œ¬√ÊÀƒ∏ˆΩ·¬€÷–£∫¢Ÿ¥Ê‘⁄ŒÞ ˝∏ˆÀƒ±þ–Œ
£¨œ¬√ÊÀƒ∏ˆΩ·¬€÷–£∫¢Ÿ¥Ê‘⁄ŒÞ ˝∏ˆÀƒ±þ–Œ![]() «∆Ω––Àƒ±þ–Œ£ª¢⁄¥Ê‘⁄ŒÞ ˝∏ˆÀƒ±þ–Œ
«∆Ω––Àƒ±þ–Œ£ª¢⁄¥Ê‘⁄ŒÞ ˝∏ˆÀƒ±þ–Œ![]() «¡‚–Œ£ª¢€¥Ê‘⁄ŒÞ ˝∏ˆÀƒ±þ–Œ
«¡‚–Œ£ª¢€¥Ê‘⁄ŒÞ ˝∏ˆÀƒ±þ–Œ![]() «æÿ–Œ£ª¢Ð¥Ê‘⁄ŒÞ ˝∏ˆÀƒ±þ–Œ
«æÿ–Œ£ª¢Ð¥Ê‘⁄ŒÞ ˝∏ˆÀƒ±þ–Œ![]() «’˝∑Ω–Œ£ªÀ˘”–’˝»∑Ω·¬€µƒ–Ú∫≈ «______£Æ
«’˝∑Ω–Œ£ªÀ˘”–’˝»∑Ω·¬€µƒ–Ú∫≈ «______£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄°˜ABC÷–£¨°œACB=90°„£¨AB=5£¨BC=3£¨P «AB±þ…œµƒ∂ص„(≤ª”ε„B÷ÿ∫œ)Ω´°˜BCP—ÿCPÀ˘‘⁄µƒ÷±œþ∑≠’€£¨µ√µΩ![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨œ¬√Ê”–Àƒ∏ˆ≈–∂œ£∫
£¨œ¬√Ê”–Àƒ∏ˆ≈–∂œ£∫
¢Ÿµ±AP=BP ±£¨![]() °ŒCP£ª
°ŒCP£ª
¢⁄µ±AP=BP ±£¨![]()
¢€µ±CP°ÕAB ±£¨![]() £ª
£ª
¢Ð![]() ≥§∂»µƒ◊Ó–°÷µ «1£Æ
≥§∂»µƒ◊Ó–°÷µ «1£Æ
À˘”–’˝»∑Ω·¬€µƒ–Ú∫≈ «( )
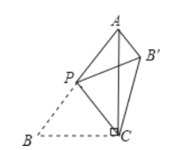
A.¢Ÿ¢€¢ÐB.¢Ÿ¢⁄C.¢Ÿ¢⁄¢ÐD.¢⁄¢€¢Ð
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥÷÷–Õ∫≈µƒµÁ»»ÀÆ∆˜π§◊˜π˝≥ûÁœ¬£∫‘⁄Ω”Õ®µÁ‘¥“‘∫Û£¨¥”≥ı ºŒ¬∂»20![]() œ¬º”»»ÀÆœ‰÷–µƒÀÆ£¨µ±ÀÆŒ¬¥ÔµΩ…Ë∂®Œ¬∂»60
œ¬º”»»ÀÆœ‰÷–µƒÀÆ£¨µ±ÀÆŒ¬¥ÔµΩ…Ë∂®Œ¬∂»60![]() ±£¨º”»»Õ£÷𣪥À∫ÛÀÆœ‰÷–µƒÀÆŒ¬ø™ º÷Ω•œ¬Ωµ£¨µ±œ¬ΩµµΩ±£Œ¬Œ¬∂»30
±£¨º”»»Õ£÷𣪥À∫ÛÀÆœ‰÷–µƒÀÆŒ¬ø™ º÷Ω•œ¬Ωµ£¨µ±œ¬ΩµµΩ±£Œ¬Œ¬∂»30![]() ±£¨‘Ÿ¥Œ◊‘∂غ”»»ÀÆœ‰÷–µƒÀÆ÷¡60
±£¨‘Ÿ¥Œ◊‘∂غ”»»ÀÆœ‰÷–µƒÀÆ÷¡60![]() £¨º”»»Õ£÷𣪵±ÀÆœ‰÷–µƒÀÆŒ¬œ¬ΩµµΩ30
£¨º”»»Õ£÷𣪵±ÀÆœ‰÷–µƒÀÆŒ¬œ¬ΩµµΩ30![]() ±£¨‘Ÿ¥Œ◊‘∂غ”»»£¨°≠°≠£¨∞¥’’“‘…œ∑Ω Ω≤ª∂œ—≠ª∑£Æ–°”Ó∏˘æð—ßœ∞∫Ø ˝µƒæ≠—È£¨∂‘∏√–Õ∫≈µÁ»»ÀÆ∆˜ÀÆœ‰÷–µƒÀÆŒ¬ÀÊ ±º‰±‰ªØµƒπʬ…Ω¯––¡ÀÃΩæø£¨∑¢œ÷ÀÆŒ¬
±£¨‘Ÿ¥Œ◊‘∂غ”»»£¨°≠°≠£¨∞¥’’“‘…œ∑Ω Ω≤ª∂œ—≠ª∑£Æ–°”Ó∏˘æð—ßœ∞∫Ø ˝µƒæ≠—È£¨∂‘∏√–Õ∫≈µÁ»»ÀÆ∆˜ÀÆœ‰÷–µƒÀÆŒ¬ÀÊ ±º‰±‰ªØµƒπʬ…Ω¯––¡ÀÃΩæø£¨∑¢œ÷ÀÆŒ¬![]() « ±º‰
« ±º‰![]() µƒ∫Ø ˝£¨∆‰÷–
µƒ∫Ø ˝£¨∆‰÷–![]() £®µ•Œª£∫
£®µ•Œª£∫![]() £©±Ì æÀÆœ‰÷–ÀƵƒŒ¬∂»£¨
£©±Ì æÀÆœ‰÷–ÀƵƒŒ¬∂»£¨![]() £®µ•Œª£∫
£®µ•Œª£∫![]() £©±Ì æΩ”Õ®µÁ‘¥∫Ûµƒ ±º‰£Æœ¬√Ê «–°”ÓµƒÃΩæøπ˝≥㨫Î≤π≥‰ÕÍ’˚£∫
£©±Ì æΩ”Õ®µÁ‘¥∫Ûµƒ ±º‰£Æœ¬√Ê «–°”ÓµƒÃΩæøπ˝≥㨫Î≤π≥‰ÕÍ’˚£∫
£®1£©–°”Óº«¬º¡À¥”≥ı ºŒ¬∂»20![]() µ⁄“ª¥Œº”»»÷¡…Ë∂®Œ¬∂»60
µ⁄“ª¥Œº”»»÷¡…Ë∂®Œ¬∂»60![]() £¨÷Æ∫ÛÀÆŒ¬¿‰»¥÷¡±£Œ¬Œ¬∂»30
£¨÷Æ∫ÛÀÆŒ¬¿‰»¥÷¡±£Œ¬Œ¬∂»30![]() µƒπ˝≥Ã÷–£¨
µƒπ˝≥Ã÷–£¨![]() ÀÊ
ÀÊ![]() µƒ±‰ªØ«Èøˆ£¨»Áœ¬±ÌÀ˘ æ£∫
µƒ±‰ªØ«Èøˆ£¨»Áœ¬±ÌÀ˘ æ£∫
Ω”Õ®µÁ‘¥∫Ûµƒ ±º‰ | 0 | 2 | 4 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | °≠ |
ÀÆœ‰÷–ÀƵƒŒ¬∂» | 20 | 30 | 40 | 60 | 51 | 45 | 40 | 36 | 33 | 30 |
¢Ÿ«Î–¥≥ˆ“ª∏ˆ∑˚∫œº”»»Ω◊∂Œ![]() ”Î
”Î![]() πÿœµµƒ∫Ø ˝Ω‚Œˆ Ω______________£ª
πÿœµµƒ∫Ø ˝Ω‚Œˆ Ω______________£ª
¢⁄∏˘æð∏√µÁ»»ÀÆ∆˜µƒπ§◊˜Ãÿµ„£¨µ±µ⁄∂˛¥Œº”»»÷¡…Ë∂®Œ¬∂»60![]() ±£¨æý¿ÎΩ”Õ®µÁ‘¥µƒ ±º‰
±£¨æý¿ÎΩ”Õ®µÁ‘¥µƒ ±º‰![]() Œ™________
Œ™________![]() £Æ
£Æ
£®2£©∏˘æð…œ ˆµƒ±Ì∏Ò£¨–°”Óª≠≥ˆ¡Àµ±![]() ±µƒ∫Ø ˝ÕºœÛ£¨«Î∏˘æð∏√µÁ»»ÀÆ∆˜µƒπ§◊˜Ãÿµ„£¨∞ÔÀ˚ª≠≥ˆµ±
±µƒ∫Ø ˝ÕºœÛ£¨«Î∏˘æð∏√µÁ»»ÀÆ∆˜µƒπ§◊˜Ãÿµ„£¨∞ÔÀ˚ª≠≥ˆµ±![]() ±µƒ∫Ø ˝ÕºœÛ£Æ
±µƒ∫Ø ˝ÕºœÛ£Æ
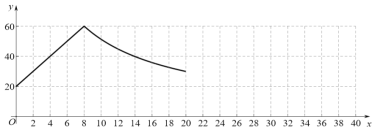
£®3£©“—÷™ “À»ÀÄ‘°µƒÀÆŒ¬‘ºŒ™![]() £¨–°”Ó‘⁄…œŒÁ8µ„’˚Ω”Õ®µÁ‘¥£¨ÀÆœ‰÷–ÀÆŒ¬Œ™20
£¨–°”Ó‘⁄…œŒÁ8µ„’˚Ω”Õ®µÁ‘¥£¨ÀÆœ‰÷–ÀÆŒ¬Œ™20![]() £¨»»ÀÆ∆˜ø™ º∞¥…œ ˆƒ£ Ωπ§◊˜£¨»Ù≤ªøº¬«∆‰À˚“ÚÀÿµƒ”∞œÏ£¨«ÎŒ ‘⁄…œŒÁ9µ„30∑÷ ±£¨»»ÀÆ∆˜µƒÀÆŒ¬______£®ÃÓ°∞ «°±ªÚ°∞∑Ò°±£© ∫œÀ˚„‘°£¨¿Ì”… «_________________£Æ
£¨»»ÀÆ∆˜ø™ º∞¥…œ ˆƒ£ Ωπ§◊˜£¨»Ù≤ªøº¬«∆‰À˚“ÚÀÿµƒ”∞œÏ£¨«ÎŒ ‘⁄…œŒÁ9µ„30∑÷ ±£¨»»ÀÆ∆˜µƒÀÆŒ¬______£®ÃÓ°∞ «°±ªÚ°∞∑Ò°±£© ∫œÀ˚„‘°£¨¿Ì”… «_________________£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº1£¨∆Ω––Àƒ±þ–ŒABCD÷–£¨AB°ÕAC£¨AB£Ω6£¨AD£Ω10£¨µ„P‘⁄±þAD…œ‘À∂Ø£¨“‘PŒ™‘≤–ƒ£¨PAŒ™∞Îæ∂µƒ°—P”Î∂‘Ω«œþACΩª”⁄A£¨E¡Ωµ„£Æ≤ªƒ—∑¢œ÷£¨ÀÊ◊≈APµƒ±‰ªØ£¨°—P”Î∆Ω––Àƒ±þ–ŒABCDµƒ±þµƒπ´π≤µ„µƒ∏ˆ ˝“≤‘⁄±‰ªØ£Æ»ÁÕº2£¨µ±°—P”αþCDœý«– ±£¨°—P”Î∆Ω––Àƒ±þ–ŒABCDµƒ±þ”–»˝∏ˆπ´π≤µ„£Æ»Ùπ´π≤µ„µƒ∏ˆ ˝Œ™4£¨‘Úœý∂‘”¶µƒAPµƒ»°÷µ∑∂ŒßŒ™_____£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com