
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
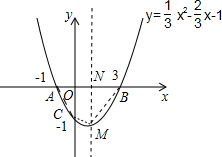 ;
;| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
| 7 |
| 3 |


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、不同的人做同一实验,得出某事件发生的概率不相同,因此该事件的概率不是确定的值 | ||
| B、实验的次数越多,某事件发生的概率就和该事件的概率越接近 | ||
C、某事件的概率为
| ||
| D、生活中常用“万一”这个词,从概率的含义说该事件的概率为“万分之一” |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知二次函数y=ax2-4x+c的图象经过点A和点B.
如图,已知二次函数y=ax2-4x+c的图象经过点A和点B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com