
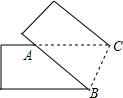
 将一张宽为4cm的矩形纸片折叠成如图所示图形,若AB=6cm,则AC的长度为6cm.
将一张宽为4cm的矩形纸片折叠成如图所示图形,若AB=6cm,则AC的长度为6cm.  学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 13.5万元 | B. | 45万元 | C. | 54万元 | D. | 100万元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 众数 | 中位数 | 平均数 | 方差 |
| 9.2 | 9.1 | 9.1 | 0.2 |
| A. | 众数 | B. | 中位数 | C. | 平均数 | D. | 方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四边形OABC是菱形,对角线OB在x轴负半轴上,位于第二象限的点A和第三象限的点C分别在双曲线y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$的一支上,分别过点A、C作y轴的垂线,垂足分别为E和F.下列结论:①|k1|=|k2|;②AE=CF;③若四边形OABC是正方形,则∠EAO=45°.其中正确的有( )
如图,四边形OABC是菱形,对角线OB在x轴负半轴上,位于第二象限的点A和第三象限的点C分别在双曲线y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$的一支上,分别过点A、C作y轴的垂线,垂足分别为E和F.下列结论:①|k1|=|k2|;②AE=CF;③若四边形OABC是正方形,则∠EAO=45°.其中正确的有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 嘉淇想证明三角形内角和是180°和其他一些的命题.请完成下列一些命题和证明.
嘉淇想证明三角形内角和是180°和其他一些的命题.请完成下列一些命题和证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com