
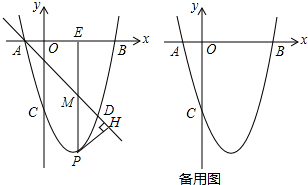
分析 (1)先由锐角三角函数的定义求得C的坐标,从而得到点B的坐标,设抛物线的解析式为y=a(x+1)(x-4),将点C的坐标代入求解即可;
(2)先求得抛物线的对称轴,从而得到点D(3,-4),然后可求得直线AD的解析式y=-x-1,故∠BAD=45°,接下来证明△PMD为等腰直角三角形,所当PM有最大值时三角形的周长最大,设P(a,a2-3a-4),M(-a-1),则PM=-a2+2a+3,然后利用配方可求得PM的最大值,最后根据△MPH的周长=(1+$\sqrt{2}$)PM求解即可;
(3)当∠EGN=90°时,如果$\frac{OA}{OC}=\frac{GN}{EG}$或$\frac{OA}{OC}=\frac{EG}{GN}$,则△AOC∽△EGN,设点G的坐标为(a,0),则N(a,a2-3a-4),则EG=a-1,NG=-a2+3a+4,然后根据题意列方程求解即可.
解答 解:(1)∵点A的坐标为(-1,0),
∴OA=1.
又∵tan∠ACO=$\frac{1}{4}$,
∴OC=4.
∴C(0,-4).
∵OC=OB,
∴OB=4
∴B(4,0).
设抛物线的解析式为y=a(x+1)(x-4).
∵将x=0,y=-4代入得:-4a=-4,解得a=1,
∴抛物线的解析式为y=x2-3x-4.
(2)∵抛物线的对称轴为x=-$\frac{-3}{2×1}$=$\frac{3}{2}$,C(0,-4),点D和点C关于抛物线的对称轴对称,
∴D(3,-4).
设直线AD的解析式为y=kx+b.
∵将A(-1,0)、D(3,-4)代入得:$\left\{\begin{array}{l}{-k+b=0}\\{3k+b=-4}\end{array}\right.$,解得k=-1,b=-1,
∴直线AD的解析式y=-x-1.
∵直线AD的一次项系数k=-1,
∴∠BAD=45°.
∵PM平行于y轴,
∴∠AEP=90°.
∴∠PMH=∠AME=45°.
∴△MPH的周长=PM+MH+PH=PM+$\frac{\sqrt{2}}{2}$MP+$\frac{\sqrt{2}}{2}$PM=(1+$\sqrt{2}$)PM.
设P(a,a2-3a-4),M(-a-1),则PM=-a-1-(a2-3a-4)=-a2+2a+3,
∵PM=-a2+2a+3=-(a-1)2+4,
∴当a=1时,PM有最大值,最大值为4.
∴△MPH的周长的最大值=4×(1+$\sqrt{2}$)=4+4$\sqrt{2}$.
(3)如图1所示;当∠EGN=90°.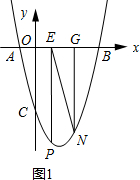
设点G的坐标为(a,0),则N(a,a2-3a-4).
∵∠EGN=∠AOC=90°,
∴$\frac{OA}{OC}=\frac{EG}{GN}$时,△AOC∽△EGN.
∴$\frac{a-1}{-{a}^{2}+3a+4}$=$\frac{1}{4}$,整理得:a2+a-8=0.
解得:a=$\frac{-1+\sqrt{33}}{2}$(负值已舍去).
∴点G的坐标为($\frac{-1+\sqrt{33}}{2}$,0).
如图2所示:当∠EGN=90°.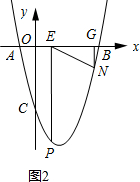
设点G的坐标为(a,0),则N(a,a2-3a-4).
∵∠EGN=∠AOC=90°,
∴$\frac{OA}{OC}=\frac{GN}{EG}$时,△AOC∽△NGE.
∴$\frac{a-1}{-{a}^{2}+3a+4}$=4,整理得:4a2-11a-17=0.
解得:a=$\frac{11+\sqrt{393}}{8}$(负值已舍去).
∴点G的坐标为($\frac{11+\sqrt{393}}{8}$,0).
∵EN在EP的右面,
∴∠NEG<90°.
如图3所示:当∠ENG′=90°时,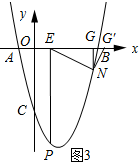
EG′=EG×$\frac{\sqrt{17}}{4}$×$\frac{\sqrt{17}}{4}$=($\frac{11+\sqrt{393}}{8}$-1)×$\frac{17}{16}$=$\frac{51+17\sqrt{393}}{128}$.
∴点G′的横坐标=$\frac{179+17\sqrt{393}}{128}$.
∵$\frac{179+17\sqrt{393}}{128}$≈4.03>4,
∴点G′不在EG上.
故此种情况不成立.
综上所述,点G的坐标为($\frac{-1+\sqrt{33}}{2}$,0)或($\frac{11+\sqrt{393}}{8}$,0).
点评 本题主要考查的是二次函数的综合应用,掌握二次函数的交点式、配方法求二次函数的最值、相似三角形的判定、等腰直角三角形的判定、一元二次方程的求根公式,列出PM的长与a的函数关系式是解题的关键.


科目:初中数学 来源: 题型:填空题
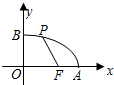 如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,点F是x轴上一点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论:①OA=5;②AF=1;③BF=5;④OB=3.其中正确结论的序号是①③.
如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,点F是x轴上一点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论:①OA=5;②AF=1;③BF=5;④OB=3.其中正确结论的序号是①③.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
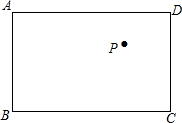 如图,在矩形ABCD中,AB=6,BC=8,P为矩形内一点,PE为点P到直线BC的距离,则PA+PD+PE的最小值为6+4$\sqrt{3}$.
如图,在矩形ABCD中,AB=6,BC=8,P为矩形内一点,PE为点P到直线BC的距离,则PA+PD+PE的最小值为6+4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知一次函数y=-$\frac{1}{2}$x+2和y=2x-3的图象分别交y轴与A、B两点,两个一次函数的图象相交于点P.
已知一次函数y=-$\frac{1}{2}$x+2和y=2x-3的图象分别交y轴与A、B两点,两个一次函数的图象相交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 汽车行驶时间x(h) | 0 | 1 | 2 | 3 | … |
| 剩余油量y(L) | 60 | 52 | 44 | 36 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com