
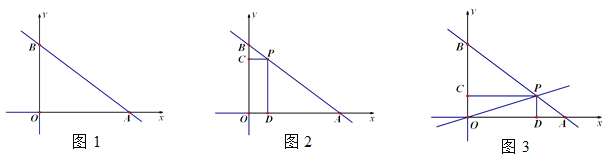
【题目】如图,在平面直角坐标系中,直线![]() 分别与x轴和y轴交于点A和点B.P是线段AB上一动点(不与A、B重合),过点P分别作PC⊥y轴于点C,PD⊥x轴于点D.设点P的横坐标为m.
分别与x轴和y轴交于点A和点B.P是线段AB上一动点(不与A、B重合),过点P分别作PC⊥y轴于点C,PD⊥x轴于点D.设点P的横坐标为m.
(1)如图1,求线段AB的长度;
(2)如图2,当![]() 时,求点P的坐标;
时,求点P的坐标;
(3)如图3,作直线OP,若直线OP的解析式为![]() ,求四边形OCPD的周长.
,求四边形OCPD的周长.
科目:初中数学 来源: 题型:
【题目】某蔬菜加工公司先后两批次收购蒜薹(tái)共100吨.第一批蒜薹价格为4000元/吨;因蒜薹大量上市,第二批价格跌至1000元/吨.这两批蒜薹共用去16万元.
(1)求两批次购进蒜薹各多少吨;
(2)公司收购后对蒜薹进行加工,分为粗加工和精加工两种:粗加工每吨利润400元,精加工每吨利润1000元.要求精加工数量不多于粗加工数量的三倍.为获得最大利润,精加工数量应为多少吨?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,点A1,B1,C1分别是BC、AC、AB的中点,A2,B2,C2分别是B1C1,A1C1,A1B1的中点,依此类推….若△ABC的周长为1,则△AnBnCn的周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
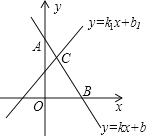
【题目】在数学学习中,及时对知识进行归纳和整理是提高学习效率的重要方法,善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,对照图形,把相关知识归纳整理如下:
一次函数与方程(组)的关系:
(1)一次函数的解析式就是一个二元一次方程;
(2)点B的横坐标是方程kx+b=0的解;
(3)点C的坐标(x,y)中x,y的值是方程组①的解.
一次函数与不等式的关系:
(1)函数y=kx+b的函数值y大于0时,自变量x的取值范围就是不等式kx+b>0的解集;
(2)函数y=kx+b的函数值y小于0时,自变量x的取值范围就是不等式②的解集.
(一)请你根据以上归纳整理的内容在下面的数字序号后写出相应的结论:① ;② ;
(二)如果点B坐标为(2,0),C坐标为(1,3);
①直接写出kx+b≥k1x+b1的解集;
②求直线BC的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知双曲线:![]() 与抛物线:y=ax2+bx+c交于A(2,3)、B(m,2)、C(﹣3,n)三点.
与抛物线:y=ax2+bx+c交于A(2,3)、B(m,2)、C(﹣3,n)三点.
(1)求双曲线与抛物线的解析式;
(2)在平面直角坐标系中描出点A、点B、点C,并求出△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=20°,∠AOC=4∠AOB,OD平分∠AOB,OM平分∠AOC,则∠MOD的度数是_____________________度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分别把下列各数填在所属的集合内:
+29,﹣3![]() ,80%,﹣1,0.3,0,﹣31415,6,
,80%,﹣1,0.3,0,﹣31415,6,![]()
(1)正数集合:{_____…};
(2)负数集合:{_____…};
(3)整数集合:{_____…};
(4)分数集合:{_____…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区为争创全国文明卫生城,2016年区政府对区绿化工程投入的资金是2000万元,2018年投的资金是2420万元,且2017年和2018年,每年投入资金的年平均增长率相同.
(1)求该区对区绿化工程投入资金的年平均增长率;
(2)若投入资金的年平均增长率不变,那么该区在2020年需投入资金多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com