
【题目】(11·湖州)(本小题10分)
我市水产养殖专业户王大爷承包了30亩水塘,分别养殖甲鱼和桂鱼,有关成本、销售情况如下表:
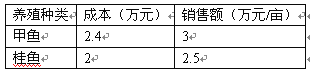
⑴2010年,王大爷养殖甲鱼20亩,桂鱼10亩,求王大爷这一年共收益多少万元?(收益=销售额-成本)
⑵2011年,王大爷继续用这30亩水塘全部养殖甲鱼和桂鱼,计划投入成本不超过70万元。若每亩养殖的成本、销售额与2010年相同,要获得最大收益,他应养殖甲鱼和桂鱼各多少亩?
⑶已知甲鱼每亩需要饲料500㎏,桂鱼每亩需要饲料700㎏,根据⑵中的养殖亩数,为了节约运输成本,实际使用的运输车辆每次装载饲料的总量是原计划每次装载总量的2倍,结果运输养殖所需要全部饲料比原计划减少了2次,求王大爷原定的运输车辆每次可装载饲料多少㎏?
【答案】解:⑴2010年王大爷的收益为:
20×(3-2.4)+10×(2.5-2)……………………………………………………2分
=17(万元)…………………………………………………………………………2分
⑵设养殖甲鱼x亩,则养殖桂鱼(30-x)亩
则题意得2.4x+2(30-x)≤70
解得x≤25,……………………………………………………………………………………2分
又设王大爷可获得收益为y万元,
则y=0.6x+0.5(30-x),
即y=![]() .…………………………………………………………………………………1分
.…………………………………………………………………………………1分
∵函数值y随x的增大而增大,
∴当x=25时,可获得最大收益。
答:要获得最大收益,应养殖甲鱼25亩,桂鱼5亩。……………………………………1分
⑶设大爷原定的运输车辆每次可装载饲料a㎏
由⑵得,共需要饲料为500×25+700×5=16000㎏,
根据题意得![]() ,……………………………………………………1分
,……………………………………………………1分
解得a=4000㎏。………………………………………………………………………1分
答:王大爷原定的运输车辆每次可装载饲料4000㎏。
【解析】略


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
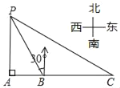
【题目】如图所示,某海盗船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处使,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,求出此时海监船与岛屿P之间的距离(即PC的长,结果精确到0.1)(参考数据:![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一种每件价格为90元的新商品,在商场试销时发现:销售单价![]() 元
元![]() 件
件![]() 与每天销售量
与每天销售量![]() 件
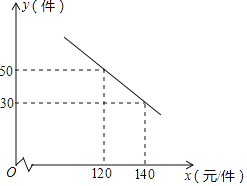
件![]() 之间满足如图所示的关系.
之间满足如图所示的关系.
![]() 求出y与x之间的函数关系式;
求出y与x之间的函数关系式;
![]() 写出每天的利润W与销售单价x之间的函数关系式,并求出售价定为多少时,每天获得的利润最大?最大利润是多少?
写出每天的利润W与销售单价x之间的函数关系式,并求出售价定为多少时,每天获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC与BD相交于点O,AB=4,BD=4![]() ,E为AB的中点,点P为线段AC上的动点,则EP+BP的最小值为( )
,E为AB的中点,点P为线段AC上的动点,则EP+BP的最小值为( )

A. 4B. 2![]() C. 2
C. 2![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年足球亚洲杯正在阿联酋进行,这项起源于我国“蹴鞠”的运动项目近年来在我国中小学校园得到大力推广,某次校园足球比赛规定:胜一场得3分,平一场得1分,负一场得0分,某足球队共进行了8场比赛,得了12分,该队获胜的场数有几种可能( )
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+ax+nb=0(1≤n≤3,n为整数),其中a是从2、4、6三个数中任取的一个数,b是从1、3、5三个数中任取的一个数,定义“方程有实数根”为事件An(n=1,2,3),当An的概率最小时,n的所有可能值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解了解节能减排、垃圾分类等知识的普及情况,从该校2000名学生中随机抽取了部分学生进行调查调查,调查结果分为“非常了解“、“了解”、“了解较少”、“不了解”四类,并将调查结果绘制出以下两幅不完整的统计图,请根据统计图回答下列问题:
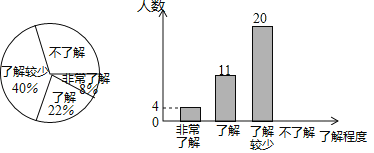
(1)本次调查的学生共有 人,估计该校2000名学生中“不了解”的人数约有 人.
(2)“非常了解”的4人中有A1,A2两名男生,B1,B2两名女生,若从中随机抽取两人去参加环保知识竞赛,请用画树状图和列表的方法,求恰好抽到2名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
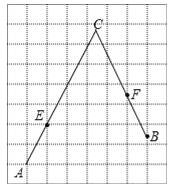
【题目】如图,在每个小正方形的边长为1的网格中,A,E为格点,B,F为小正方形边的中点,C为AE,BF的延长线的交点.
(Ⅰ)AE的长等于 ;
(Ⅱ)若点P在线段AC上,点Q在线段BC上,且满足AP=PQ=QB,请在如图所示的网格中,用无刻度的直尺,画出线段PQ,并简要说明点P,Q的位置是如何找到的(不要求证明) .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com