
定义:底与腰的比是 的等腰三角形叫做黄金等腰三角形.
的等腰三角形叫做黄金等腰三角形.
如图,已知△ABC中,AB=BC,∠C=36°,BA1平分∠ABC交AC于A1.
(1)证明:AB2=AA1•AC;
(2)探究:△ABC是否为黄金等腰三角形?请说明理由;(提示:此处不妨设AC=1)
(3)应用:已知AC=a,作A1B1∥AB交BC于B1,B1A2平分∠A1B1C交AC于A2,作A2B2∥AB交B2,B2A3平分∠A2B2C交AC于A3,作A3B3∥AB交BC于B3,…,依此规律操作下去,用含a,n的代数式表示An﹣1An.(n为大于1的整数,直接回答,不必说明理由)

解答: (1)证明:∵AC=BC,∠C=36°,
∴∠A=∠ABC=72°,
∵BA1平分∠ABC,
∴∠ABA1=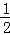 ∠ABC=36°,
∠ABC=36°,
∴∠C=∠ABA1,
又∵∠A=∠A,
∴△ABC∽△AA1B,
∴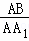 =
=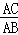 ,即AB2=AA1•AC;
,即AB2=AA1•AC;
(2)解:△ABC是黄金等腰三角形,
理由:由(1)知,AB2=AC•AA1,
设AC=1,
∴AB2=AA1,
又由(1)可得:AB=A1B,
∵∠A1BC=∠C=36°,
∴A1B=A1C,
∴AB=A1C,
∴AA1=AC﹣A1C=AC﹣AB=1﹣AB,
∴AB2=1﹣AB,
设AB=x,即x2=1﹣x,
∴x2+x﹣1=0,
解得:x1=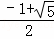 ,x2=
,x2=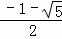 (不合题意舍去),
(不合题意舍去),
∴AB=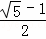 ,
,
又∵AC=1,
∴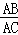 =
=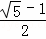 ,
,
∴△ABC是黄金等腰三角形;
(3)解:由(2)得;当AC=a,则AA1=AC﹣A1C=AC﹣AB=a﹣AB=a﹣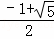 a=
a=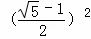 a,
a,
同理可得:A1A2=A1C﹣A1B1=AC﹣AA1﹣A1B1
=a﹣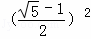 a﹣
a﹣ A1C
A1C
=a﹣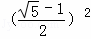 a﹣
a﹣ [a﹣
[a﹣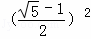 a]
a]
=( )3a.
)3a.
故An﹣1An=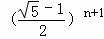 a.
a.



科目:初中数学 来源: 题型:
某商店举办促销活动,促销的方法是将原价x元的衣服以(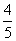 x-10) 元出售,则下列说法中,能正确表达该商店促销方法的是
x-10) 元出售,则下列说法中,能正确表达该商店促销方法的是
A. 原价减去10元后再打8折  B. 原价打8折后再减去10元
B. 原价打8折后再减去10元
C. 原价减去10元后再打2折 D . 原价打2折后再减去10元
. 原价打2折后再减去10元
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读下列材料,并用相关的思想方法解决问题.
计算:(1﹣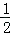 ﹣
﹣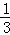 ﹣
﹣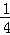 )×(
)×(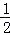 +
+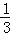 +
+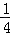 +
+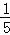 )﹣(1﹣
)﹣(1﹣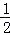 ﹣
﹣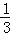 ﹣
﹣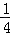 ﹣
﹣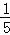 )×(
)×(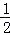 +
+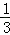 +
+ ).
).
令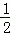 +
+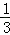 +
+ =t,则
=t,则
原式=(1﹣t)(t+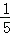 )﹣(1﹣t﹣
)﹣(1﹣t﹣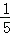 )t
)t
=t+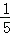 ﹣t2﹣
﹣t2﹣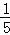 t﹣
t﹣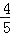 t+t2
t+t2
=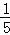
问题:
(1)计算
(1﹣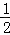 ﹣
﹣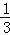 ﹣
﹣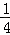 ﹣…﹣
﹣…﹣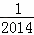 )×(
)×(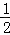 +
+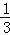 +
+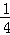 +
+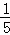 +…+
+…+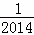 +
+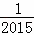 )﹣(1﹣
)﹣(1﹣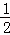 ﹣
﹣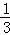 ﹣
﹣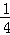 ﹣
﹣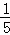 ﹣…﹣
﹣…﹣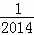 ﹣
﹣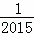 )×(
)×(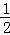 +
+ +
+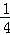 +…+
+…+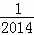 );
);
(2)解方程(x2+5x+1)(x2+5x+7)=7.
查看答案和解析>>
科目:初中数学 来源: 题型:
近年来,“在初中数学教学中使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了若干名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和统计图:
学生对使用计算器影响计算能力发展的看法统计表
看法 没有影响 影响不大 影响很大
学生人数 100 60 m
根据以上图表信息,解答下列问题:
(1)统计表中的m= ;
(2)统计图中表示“影响不大”的扇形的圆心角度数为 度;
(3)从这次接受调查的学生中随机调查一人,恰好是持“影响很大”看法的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
为迎接“六一”儿童节,某儿童品牌玩具专卖店购进了A、B两类玩具,其中A类玩具的进价比B类玩具的进价每个多3元,经调查:用900元购进A类玩具的数量与用750元购进B类玩具的数量相同.设A类玩具的进价为m元/个,根据题意可列分式方程为( )
A. 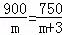 B.
B. 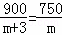 C.
C. 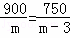 D.
D. 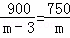
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com