
【题目】如图,在矩形ABCD中,AD=2![]() , AB=1.将矩形ABCD对折,得到折痕MN;沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G.下列结论:①△CMP是直角三角形;②点C、E、G不在同一条直线上;③PC=
, AB=1.将矩形ABCD对折,得到折痕MN;沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G.下列结论:①△CMP是直角三角形;②点C、E、G不在同一条直线上;③PC=![]() MP;④BP=
MP;④BP=![]() ;⑤点F是△CMP外接圆的圆心,其中正确的个数为( )
;⑤点F是△CMP外接圆的圆心,其中正确的个数为( )
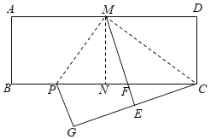
A. 2个B. 3个C. 4个D. 5个
【答案】B
【解析】
根据折叠的性质得到∠DMC=∠EMC,∠AMP=∠EMP,于是得到∠PME+∠CME=![]() ×180°=90°,求得△CMP是直角三角形;故①正确;根据平角的定义得到点C、E、G在同一条直线上,故②错误,AB=1,则AD=2
×180°=90°,求得△CMP是直角三角形;故①正确;根据平角的定义得到点C、E、G在同一条直线上,故②错误,AB=1,则AD=2![]() ,得到DM=
,得到DM=![]() AD=
AD=![]() ,根据勾股定理得到CM=
,根据勾股定理得到CM=![]() =
=![]() ,根据射影定理得到CP=
,根据射影定理得到CP=![]() =
=![]() ,得到PC=
,得到PC=![]() MP,故③错误;求得PB=
MP,故③错误;求得PB=![]() AB=
AB=![]() ,故④正确,根据平行线等分线段定理得到CF=PF,求得点F是△CMP外接圆的圆心,故⑤正确.
,故④正确,根据平行线等分线段定理得到CF=PF,求得点F是△CMP外接圆的圆心,故⑤正确.
解:∵沿着CM折叠,点D的对应点为E,
∴∠DMC=∠EMC,
∵再沿着MP折叠,使得AM与EM重合,折痕为MP,
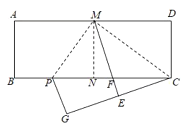
∴∠AMP=∠EMP,
∵∠AMD=180°,
∴∠PME+∠CME=![]() ×180°=90°,
×180°=90°,
∴△CMP是直角三角形;故①正确;
∵沿着CM折叠,点D的对应点为E,
∴∠D=∠MEC=90°,
∵再沿着MP折叠,使得AM与EM重合,折痕为MP,
∴∠MEG=∠A=90°,
∴∠GEC=180°,
∴点C、E、G在同一条直线上,故②错误;
∵AD=2![]() AB,
AB,
∵AB=1,则AD=2![]() ,
,
∵将矩形ABCD对折,得到折痕MN;
∴DM=![]() AD=
AD=![]()
∴CM=![]() =
=![]() ,
,
∵∠PMC=90°,MN⊥PC,
∴CM2=CNCP,
∴CP=![]() =
=![]() ,
,
∴PN=CPCN=![]()
∴PM=![]() =
=![]()
∴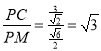 ,
,
∴PC=![]() MP,故③错误;
MP,故③错误;
∵PC=![]() AB=
AB=![]() ,
,
∴PB=![]() -
-![]() =
=![]()
故④正确,
∵CD=CE,EG=AB,AB=CD,
∴CE=EG,
∵∠CEM=∠G=90°,
∴FE∥PG,
∴CF=PF,
∵∠PMC=90°,
∴CF=PF=MF,
∴点F是△CMP外接圆的圆心,故⑤正确;
故选:B.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
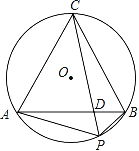
【题目】如图,将线段AB绕点A逆时针旋转60°得AC,连接BC,作△ABC的外接圆⊙O,点P为劣弧![]() 上的一个动点,弦AB、CP相交于点D.
上的一个动点,弦AB、CP相交于点D.
(1)求∠APB的大小;
(2)当点P运动到何处时,PD⊥AB?并求此时CD:CP的值;
(3)在点P运动过程中,比较PC与AP+PB的大小关系,并对结论给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为( )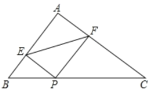
A. 2B. 2.4C. 2.5D. 2.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形AOBC,A(0,3)、B(6,0),点E在OB上,∠AEO=30°,点P从点Q(﹣4,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t秒.
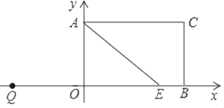
(1)求点E的坐标;
(2)当△PAE是等腰三角形时,求t的值;
(3)以点P为圆心,PA为半径的⊙P随点P的运动而变化,当⊙P与四边形AEBC的边(或边所在的直线)相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市一月份的营业额为200万元,一月、二月、三月的营业额共1000万元,如果平均每月增长率为![]() ,则由题意列方程应为____________________________ 。
,则由题意列方程应为____________________________ 。
查看答案和解析>>
科目:初中数学 来源: 题型:
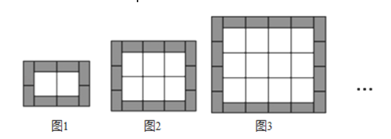
【题目】如图,中间用相同的白色正方形瓷砖,四周用相同的黑色长方形瓷砖铺设矩形地面,请观察图形并解答下列问题.
(1)问:依据规律在第6个图中,黑色瓷砖多少块,白色瓷砖有多少块;
(2)某新学校教室要装修,每间教室面积为68m2 , 准备定制边长为0.5米的正方形白色瓷砖和长为0.5米、宽为0.25米的长方形黑色瓷砖来铺地面.按照此图案方式进行装修,瓷砖无须切割,恰好完成铺设.已知白色瓷砖每块20元,黑色瓷砖每块10元,请问每间教室瓷砖共需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD 是菱形ABCD 的对角线,∠A=30°.
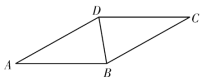
(1)请用尺规作图法,作AB 的垂直平分线EF,垂足为E,交AD 于F;(不要 求写作法,保留作图痕迹)
(2)在(1)的条件下,连接BF,求∠DBF 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杨老师为了了解所教班级学生课后复习的具体情况,对本班部分学生进行了一个月的跟踪调查,然后将调查结果分成四类:A:优秀;B:良好;C:一般;D:较差.并将调查结果绘制成以下两幅不完整的统计图.
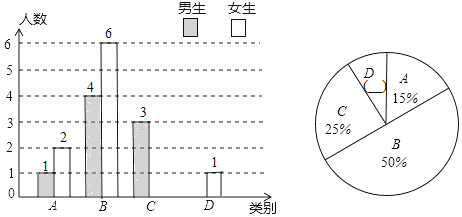
请根据统计图解答下列问题:
(1)本次调查中,杨老师一共调查了 名学生,其中C类女生有 名,D类男生有 名;
(2)补全上面的条形统计图和扇形统计图;
(3)在此次调查中,小平属于D类.为了进步,她请杨老师从被调查的A类学生中随机选取一位同学,和她进行“一帮一”的课后互助学习.请求出所选的同学恰好是一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则![]() .下面是这个定理的部分证明过程.
.下面是这个定理的部分证明过程.

证明:如图2,过C作CE∥DA.交BA的延长线于E.…
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,求△ABD的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com