
【题目】如图,矩形AOBC,A(0,3)、B(6,0),点E在OB上,∠AEO=30°,点P从点Q(﹣4,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t秒.
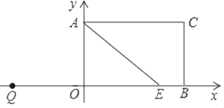
(1)求点E的坐标;
(2)当△PAE是等腰三角形时,求t的值;
(3)以点P为圆心,PA为半径的⊙P随点P的运动而变化,当⊙P与四边形AEBC的边(或边所在的直线)相切时,求t的值.
【答案】(1)点E的坐标为(![]() ,0);(2)当△PAE是等腰三角形时,t的值为(3
,0);(2)当△PAE是等腰三角形时,t的值为(3![]() ﹣2)s或(3
﹣2)s或(3![]() )s或(4+
)s或(4+![]() )s;(3),当⊙P与四边形AEBC的边(或边所在的直线)相切时,t的值为(4﹣
)s;(3),当⊙P与四边形AEBC的边(或边所在的直线)相切时,t的值为(4﹣![]() )秒或4秒或
)秒或4秒或![]() 秒.
秒.
【解析】
(1)由A,B的坐标及∠AEO=30°可得OE=![]() ,即可求出点E的坐标;
,即可求出点E的坐标;
(2)分三种情形①当EA=EP时,EP1=EA=EP2=6,求出t.②当PA=PE时,设P3E=P3E=x,在Rt△AOP3中,32+(![]() -x)2=x2,x=2
-x)2=x2,x=2![]() ,求出t即可.③当AE=AP时,点P在点Q左边,不符合题意.
,求出t即可.③当AE=AP时,点P在点Q左边,不符合题意.
(3)本小题分三种情况讨论:①当PA⊥AE时,⊙P与AE相切;②当PA⊥AC时,⊙P与AC相切;③当PB⊥BC时,⊙P与BC相切;分别求出各种情况的t的值.
(1)∵A(0,3),B(6,0),
∴OA=3,OB=6,
∵∠AEO=30°,
∴OE=![]() OA=3
OA=3![]() ,
,
∴点E的坐标为(3![]() ,0).
,0).
(2)如图1中,
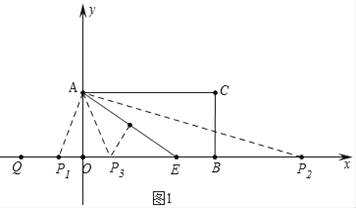
当EA=EP时,EP1=EA=EP2=6,此时t=3![]() ﹣2或3
﹣2或3![]() +10,
+10,
当PA=PE时,设P3E=P3E=x,在Rt△AOP3中,32+(3![]() ﹣x)2=x2,
﹣x)2=x2,
∴x=2![]() ,此时t=4+
,此时t=4+![]()
当AE=AP时,点P在点Q左边,不符合题意.
综上所述,当△PAE是等腰三角形时,t的值为(3![]() ﹣2)s或(3
﹣2)s或(3![]() )s或(4+
)s或(4+![]() )s.
)s.
(3)由题意知,若⊙P与四边形AEBC的边相切,有以下三种情况:
①如图2中,当PA⊥AE时,⊙P与AE相切,
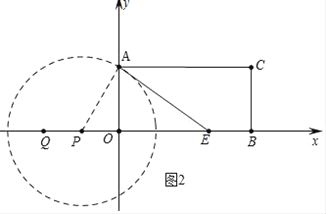
∵∠AEO=30°,AO=3,
∴∠APO=60°,
∴OP=![]() ,
,
∴QP=QO﹣PO=4﹣![]() ,
,
∵点P从点Q(﹣4,0)出发,沿x轴向右以每秒1个单位的速度运动,
∴t=4﹣![]() (秒).
(秒).
②如图3中,当PA⊥AC时,⊙P与AC相切,
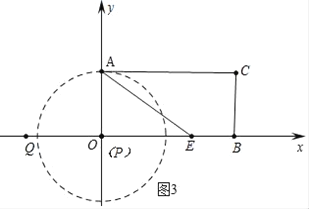
∵QO=4,点P从点Q(﹣4,0)出发,沿x轴向右以每秒1个单位的速度运动,
∴t=4(秒),
③如图4中,当⊙P与BC相切时,
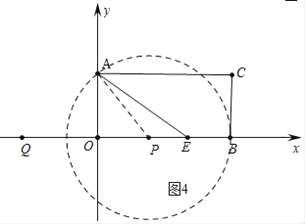
由题意,PA2=PB2=(10﹣t)2,PO2=(t﹣4)2.
于是(10﹣t)2=(t﹣4)2+32.
解得t=![]() (秒),
(秒),
综上所述,当⊙P与四边形AEBC的边(或边所在的直线)相切时,t的值为(4﹣![]() )秒或4秒或
)秒或4秒或![]() 秒.
秒.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在宁波慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图。

(1)这50名同学捐款的众数为___元,中位数为___元;
(2)该校共有600名学生参与捐款,请估计该校学生的捐款总数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小李从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好能围成一个容积为35 m3的无盖长方体箱子,且此长方体箱子的底面长比宽多2m,现己知购买这种铁皮每平方米需30元钱,问小李购回这张矩形铁皮共花了多少元钱?

查看答案和解析>>
科目:初中数学 来源: 题型:
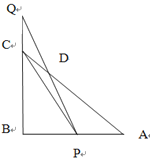
【题目】如图,等腰Rt△ABC的直角边AB=2,点P、Q分别从A、C两点同时出发,以相等的速度作直线运动,已知点P沿射线AB运动,点Q沿边BC的延长线运动,PQ与直线相交于点D.
(1)设AP的长为x,△PCQ的面积为S,求出S关于x的函数关系式;
(2)当AP的长为何值时,![]() =
=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
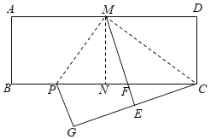
【题目】如图,在矩形ABCD中,AD=2![]() , AB=1.将矩形ABCD对折,得到折痕MN;沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G.下列结论:①△CMP是直角三角形;②点C、E、G不在同一条直线上;③PC=
, AB=1.将矩形ABCD对折,得到折痕MN;沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G.下列结论:①△CMP是直角三角形;②点C、E、G不在同一条直线上;③PC=![]() MP;④BP=
MP;④BP=![]() ;⑤点F是△CMP外接圆的圆心,其中正确的个数为( )
;⑤点F是△CMP外接圆的圆心,其中正确的个数为( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌相机,原售价每台4000元,经连续两次降价后,现售价每台3240元,已知两次降价的百分率一样。
(1)求每次降价的百分率;
(2)如果按这个百分率再降价一次,求第三次降价后的售价?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com