练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
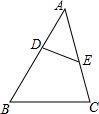
    4．如图，在△ABC中，点D，E分别是AB，AC边上的两个点，且$\frac{AE}{AB}=\frac{AD}{AC}=\frac{1}{2}$，则S△ADE：S△ABC的值为（　　）
    A．1：$\sqrt{3}$B．1：2C．1：3D．1：4

    分析 根据条件$\frac{AE}{AB}=\frac{AD}{AC}=\frac{1}{2}$，和公共角相等可证明△ADE∽△ACB，由相似三角形的性质：对应边的比值相等即可求出DE的长．

    解答 解：∵$\frac{AE}{AB}=\frac{AD}{AC}=\frac{1}{2}$，∠A=∠A，
    ∴△ADE∽△ACB，
    ∴S△ADE：S△ABC=（$\frac{1}{2}$）2=$\frac{1}{4}$．
    故选D．

    点评 本题考查了相似三角形的判定和性质，是中考常见题型，比较简单．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．如图所示，现有一圆心角为90°、半径为80cm的扇形铁片，用它恰好围成一个圆锥形的量筒；如果用其它铁片再做一个圆形盖子把量筒底面密封．（接缝都忽略不计）．
    求：（1）该圆锥盖子的半径为多少cm？
    （2）制作这个密封量筒，共用铁片多少cm2．（注意：结果保留π）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．已知：AD是∠BAC的平分线，FE是AD中垂线，求证：ED2=EB•EC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

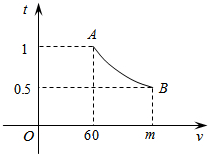    12．一辆汽车匀速通过某段公路，所需时间t（h）与行驶速度v（km/h）满足函数关系：t=$\frac{k}{v}$其图象为如图所示的一段曲线且端点为A（60，1），和B（m，0.5）
    （1）求k和m的值．
    （2）若行驶速度不得超过80km/h，则汽车通过该路段最少需要多少时间．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

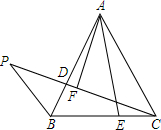    19．已知：等边△ABC，D，E分别是AB，BC上的点，且BD=CE，过点A向CD作垂线，垂足为F，延长CD到点P，连接PB，使∠P=30°，求证：PF=CF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．下列说法正确的是（　　）
    A．延长射线OPB．延长直线CDC．延长线段CDD．反向延长直线DC

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．若点A（3，-4）、B（-2，m）在同一个反比例函数的图象上，则m的值为6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

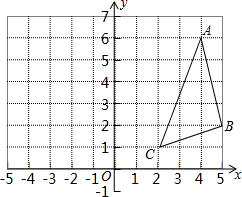    13．如图，△ABC的顶点坐标分别为A（4，6），B（5，2），C（2，1），
    （1）作出△ABC关于y轴对称的△A′B′C′，并写出A′，B′，C′的坐标．
    （2）求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．根据下列语句画出图形．
    （1）线段AB与直线1相交于点P；
    （2）射线0A经过A，B，C三点，点C在点A与点B之间；
    （3）点P在线段AB上，且AP=2BP．

    查看答案和解析>>

    同步练习册答案