
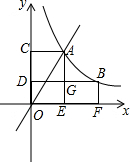 如图,直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,a),点B是反比例函数图象上的任意一点(不与A点重合).
如图,直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,a),点B是反比例函数图象上的任意一点(不与A点重合).分析 (1)把点A坐标代入两个函数解析式即可解决问题.
(2)由四边形ACOE与四边形DBFO面积相等即可证明.
解答 解(1)∵直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,a),
∴a=2×1=2,2=$\frac{k}{1}$,
∴a=2,k=2,
∴反比例函数为y=$\frac{2}{x}$.
(2)结论:s1=s2.
设A(m,n),B(a,b),
∵A、B在反比例函数图象上,
∴mn=2,ab=2,
∵S四边形ACOE=mn=2,S四边形DBFO=ab=2,
∴S四边形ACOE=S四边形DBFO,
∴S四边形ACDG=S四边形BFEG,
即s1=s2.
点评 本题考查一次函数与反比例函数的交点问题,学会待定系数法确定函数解析式,理解反比例函数中比例系数K的几何意义,属于中考常考题型.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等于5cm | B. | 小于5cm | C. | 小于或等于5cm | D. | 大于或等于5cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $2\sqrt{2}-\sqrt{2}=2$ | B. | $2\sqrt{2}-\sqrt{2}=1$ | C. | $2\sqrt{2}-\sqrt{2}=\sqrt{2}$ | D. | $2\sqrt{2}-\sqrt{2}=0$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com