
 如图,在面积为4的等边△ABC的BC边上有一点D,连接AD,以AD为边作等边△ADE,连接BE.则四边形AEBD的面积是4.
如图,在面积为4的等边△ABC的BC边上有一点D,连接AD,以AD为边作等边△ADE,连接BE.则四边形AEBD的面积是4. 分析 根据等边三角形的性质得到AE=AD,AB=AC,∠BAC=∠DAE=60°,于是得到∠EAB=∠DAC,推出△AEB≌△ADC,得到S△AEB=S△ADC,即可得到结论.
解答 解:∵△ABC与△ADE是等边三角形,
∴AE=AD,AB=AC,∠BAC=∠DAE=60°,
∴∠EAB=∠DAC,
在△AEB与△ADC中,
$\left\{\begin{array}{l}{AE=AD}\\{∠EAB=∠DAC}\\{AB=AC}\end{array}\right.$,
∴△AEB≌△ADC,
∴S△AEB=S△ADC,
∴四边形AEBD的面积=等边△ABC的面积=4.
故答案为:4.
点评 本题考查了全等三角形的判定和性质,图形的面积的计算,等边三角形的性质,熟练掌握全等三角形的判定和性质是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$+$\sqrt{5}$=$\sqrt{8}$ | B. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | C. | $\sqrt{(-3)^{2}}$=-3 | D. | $\sqrt{7}$-$\sqrt{5}$=$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
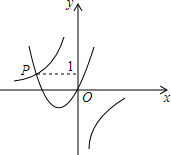 如图,已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解是x=-3.
如图,已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解是x=-3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
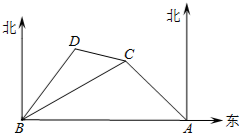 2016年1月6日,我国南沙永暑礁新建港口、机场完成试航试飞,将为岛礁物资运输、人员往来、通信导航、救援补给提供便捷支持,使航行和飞行更为安全可靠.如图所示,永暑礁新建港口在A处,位于港口A的正西方的有一小岛B,小岛C在小岛B的北偏东60°方向,小岛C在A的北偏西45°方向;小岛D在小岛B的北偏东38°方向且满足∠BCD=37°,港口A和小岛C的距离是23$\sqrt{2}$km.
2016年1月6日,我国南沙永暑礁新建港口、机场完成试航试飞,将为岛礁物资运输、人员往来、通信导航、救援补给提供便捷支持,使航行和飞行更为安全可靠.如图所示,永暑礁新建港口在A处,位于港口A的正西方的有一小岛B,小岛C在小岛B的北偏东60°方向,小岛C在A的北偏西45°方向;小岛D在小岛B的北偏东38°方向且满足∠BCD=37°,港口A和小岛C的距离是23$\sqrt{2}$km.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com