
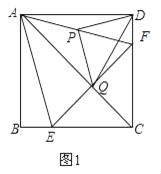
【题目】如图1,在正方形ABCD中,点E、F分别在边BC,CD上,且BE=DF,点P是AF的中点,点Q是直线AC与EF的交点,连接PQ,PD.
(1)求证:AC垂直平分EF;
(2)试判断△PDQ的形状,并加以证明;
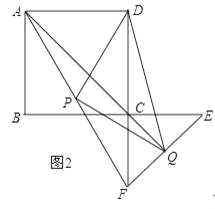
(3)如图2,若将△CEF绕着点C旋转180°,其余条件不变,则(2)中的结论还成立吗?若成立,请加以证明;若不成立,请说明理由.
【答案】(1)证明见解析;(2)△PDQ是等腰直角三角形;理由见解析(3)成立;理由见解析.
【解析】试题(1)由正方形的性质得出AB=BC=CD=AD,∠B=∠ADF=90°,∠BCA=∠DCA=45°,由BE=DF,得出CE=CF,△CEF是等腰直角三角形,即可得出结论;
(2)由直角三角形斜边上的中线的性质得出PD=![]() AF,PQ=
AF,PQ=![]() AF,得出PD=PQ,再证明∠DPQ=90°,即可得出结论;
AF,得出PD=PQ,再证明∠DPQ=90°,即可得出结论;
(3)由直角三角形斜边上的中线的性质得出PD=![]() AF,PQ=
AF,PQ=![]() AF,得出PD=PQ,再证明点A、F、Q、P四点共圆,由圆周角定理得出∠DPQ=2∠DAQ=90°,即可得出结论.
AF,得出PD=PQ,再证明点A、F、Q、P四点共圆,由圆周角定理得出∠DPQ=2∠DAQ=90°,即可得出结论.
试题解析:(1)证明:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠ADF=90°,∠BCA=∠DCA=45°,
∵BE=DF,
∴CE=CF,
∴AC垂直平分EF;
(2)解:△PDQ是等腰直角三角形;理由如下:
∵点P是AF的中点,∠ADF=90°,
∴PD=![]() AF=PA,
AF=PA,
∴∠DAP=∠ADP,
∵AC垂直平分EF,
∴∠AQF=90°,
∴PQ=![]() AF=PA,
AF=PA,
∴∠PAQ=∠AQP,PD=PQ,
∵∠DPF=∠PAD+∠ADP,∠QPF=∠PAQ+∠AQP,
∴∠DPQ=2∠PAD+2∠PAQ=2(∠PAD+∠PAQ)=2×45°=90°,
∴△PDQ是等腰直角三角形;
(3)成立;理由如下:
∵点P是AF的中点,∠ADF=90°,
∴PD=![]() AF=PA,
AF=PA,
∵BE=DF,BC=CD,∠FCQ=∠ACD=45°,∠ECQ=∠ACB=45°,
∴CE=CF,∠FCQ=∠ECQ,
∴CQ⊥EF,∠AQF=90°,
∴PQ=![]() AF=AP=PF,
AF=AP=PF,
∴PD=PQ=AP=PF,
∴点A、F、Q、P四点共圆,
∴∠DPQ=2∠DAQ=90°,
∴△PDQ是等腰直角三角形.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
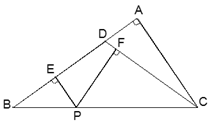
【题目】如图,在△ABC中,∠A=90°, D是AB边上一点,且DB=DC,过BC上一点P(不包括B,C二点)作PE⊥AB,垂足为点E, PF⊥CD,垂足为点F,已知AD:DB=1:4,BC=![]() ,求PE+PF的长.
,求PE+PF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划购买一批课外读物,为了了解学生对课外读物的需求情况,学校进行了一次“我最喜爱的课外读物”的调查,设置了“文学”、“科普”、“艺术”和“其他”四个类别,规定每人必须并且只能选择其中一类,现从全体学生的调查表中随机抽取了部分学生的调查表进行统计,并把统计结果绘制了如图所示的两幅不完整的统计图.
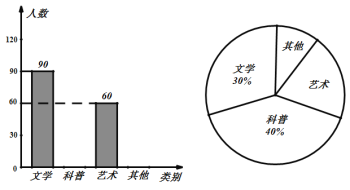
(1) 从全体学生的调查表中随机抽取了多少名学生?
(2) 将条形图补充完整;
(3) 艺术类读物所在扇形的圆心角是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
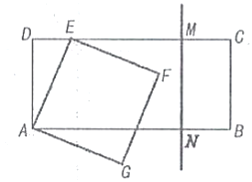
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() .点
.点![]() 从
从![]() 向
向![]() 以每秒
以每秒![]() 个单位的速度运动,以
个单位的速度运动,以![]() 为一边在
为一边在![]() 的右下方作正方形
的右下方作正方形![]() .同时垂直于
.同时垂直于![]() 的直线
的直线![]() 从
从![]() 向
向![]() 以每秒
以每秒![]() 个单位的速度运动,设运动时间为
个单位的速度运动,设运动时间为![]() 秒,当
秒,当![]() ________.秒时,直线
________.秒时,直线![]() 和正方形
和正方形![]() 开始有公共点
开始有公共点
查看答案和解析>>
科目:初中数学 来源: 题型:
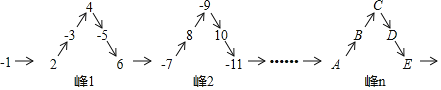
【题目】将一列有理数﹣1,2,﹣3,4,﹣5,6,…如图所示有序排列,根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么,“峰6”中C的位置是有理数_____,﹣2019应排在A、B、C、D、E中的_____位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种盛酒的桶,已知10个大桶加上2个小桶可以盛酒6斛(斛,音hu,是古代的一种容量单位),3个大桶加上15个小桶也可以盛酒6斛.
(1)求1个大桶可盛酒多少斛?
(2)分析2个大桶加上3个小桶可以盛酒2斛吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com