
 阅读下列材料:
阅读下列材料:分析 首先根据题意画出图形,然后由AC是四边形ABCD的和谐线,可以得出△ACD是等腰三角形,从图1,图2,图3三种情况运用等边三角形的性质,正方形的性质和30°的直角三角形性质就可以求出∠ABC的度数.
解答 解:∵AC是四边形ABCD的和谐线,
∴△ACD是等腰三角形,
在等腰Rt△ABD中,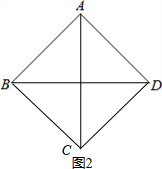
∵AB=AD,
∴AB=AD=BC,
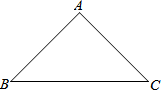
如图1,当AD=AC时,
∴AB=AC=BC,∠ACD=∠ADC
∴△ABC是正三角形,
∴∠ABC=60°.
如图2,当AD=CD时,
∴AB=AD=BC=CD.
∵∠BAD=90°,
∴四边形ABCD是正方形,
∴∠ABC=90°;
如图3,当AC=CD时,过点C作CE⊥AD于E,过点B作BF⊥CE于F,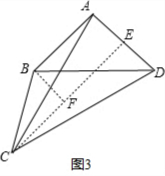
∵AC=CD.CE⊥AD,
∴AE=$\frac{1}{2}$AD,∠ACE=∠DCE.
∵∠BAD=∠AEF=∠BFE=90°,
∴四边形ABFE是矩形.
∴BF=AE.
∵AB=AD=BC,
∴BF=$\frac{1}{2}$BC,
∴∠BCF=30°.
∵AB=BC,
∴∠ACB=∠BAC.
∵AB∥CE,
∴∠BAC=∠ACE,
∴∠ACB=∠BAC=$\frac{1}{2}$∠BCF=15°,
∴∠ABC=150°,
综上:∠ABC的度数可能是:60°90°150°.
点评 此题考查了等腰直角三角形的性质,等腰三角形的性质、矩形的性质、正方形的性质,菱形的性质,此题难度较大,注意掌握数形结合思想与分类讨论思想的应用.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速度继续向甲地行驶,到达甲地后停止行驶;快车达到乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程y(千米)与所用时间x(小时)之间的函数图象如图.请结合图象信息解答下列问题:
快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速度继续向甲地行驶,到达甲地后停止行驶;快车达到乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程y(千米)与所用时间x(小时)之间的函数图象如图.请结合图象信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
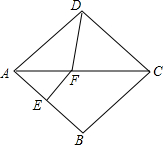 如图所示,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
如图所示,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )| A. | 75° | B. | 70° | C. | 60° | D. | 55° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com