
【题目】如图,已知在Rt△ABC中,∠C=90°,以BC为直径的⊙O交斜边AB于点E,若D是AC的中点,连结DE.
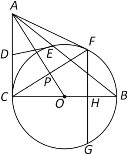
(1)求证:DE为⊙O的切线;
(2)若![]() ,
,![]() ,求⊙O的半径长;
,求⊙O的半径长;
(3)在(2)的条件下,过点A作⊙O的另一条切线,切点为F,过点F作FG⊥BC,垂足为H,且交⊙O于G点,连结AO 交CF于点P.求线段FG的长度.
【答案】(1)详见解析;(2)2;(3)![]() ;
;
【解析】
(1)连接OE、OD,易证OD是△ABC的中位线,利用中位线的性质可证明△COD≌△EOD, 所以∠DEO=∠DCO =90°,从而可知DE是⊙O的切线;
(2)由切线长定理得:DC=DE=![]() ,由点M是AC的中点可知AC=3,tan∠ABC=
,由点M是AC的中点可知AC=3,tan∠ABC=![]() ,所以BC=4,从而可知⊙O的半径为2;
,所以BC=4,从而可知⊙O的半径为2;
(3连结OF,由AC、AF都是⊙O的切线可知AO⊥CF,利用等面积可求得CF的长度,设OH为x,然后利用勾股定理可求得OH的长度,利用垂径定理即可求得FG.
(1)证明:连结OE、OD,
∵D是AC的中点,O是BC的中点,
∴OD是△ABC的中位线,
∴OD∥AB,
∴∠COD=∠ABC,∠EOD=∠OEB,
又∵OB=OE,∴∠OEB=∠ABC,
∴∠COD=∠EOD,
在△COD与△EOD中,
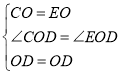
∴△COD≌△EOD(SAS),
∴∠DEO=∠DCO =90°,
∴DE是⊙O的切线.
(2)∵DC、DE分别是⊙O的切线,
∴![]() ,
,
∵D是AC的中点,
∴AC=2DC=3,
在Rt△ABC中,
∵![]() ,∴
,∴![]() ,
,
∴BC=4,
∴⊙O的半径为2.
(3)连结OF,
∵AC、AF都是⊙O的切线,
∴AC=AF,AO平分∠CAF,
∴AO⊥CF,且PC=PF,
∵AC=3,OC=2,
∴由勾股定理可得:![]() ,
,
由三角形面积法可得:![]() ACOC=
ACOC=![]() AOCP,
AOCP,
∴CP=![]() ,∴CF=
,∴CF=![]() ,
,
设OH=x,则CH=x+2,
由勾股定理可得:![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
在Rt△CFH中,
由勾股定理可得:![]() ,
,
∴由垂径定理可得:![]() .
.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】某地教育部门为学生提供了四种在线学习方式:阅读、听课、答疑、讨论,并对部分学生作了“最感兴趣的在线学习方式”网络调查(只选择一类),把调查结果绘制成如下两幅尚不完整的统计图:

根据图中信息,回答下列问题:
(1)本次调查的人数有 人;在扇形统计图中,“在线答疑”所在扇形的圆心角度数是 ;
(2)补全条形统计图;
(3)在随机调查的学生中,甲、乙两位同学选择同类“最感兴趣的在线学习方式”的概率是否等于![]() ?说明理由.
?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
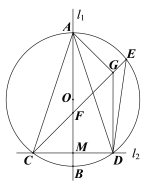
【题目】如图,直线l1⊥l2于点M,以l1上的点O为圆心画圆,交l1于点A,B,交l2于点C,D,OM=4,CD=6,点E为![]() 上的动点,CE交AB于点F,AG⊥CE于点G,连接DG,AC,AD.
上的动点,CE交AB于点F,AG⊥CE于点G,连接DG,AC,AD.
(1)求⊙O的半径长;
(2)若DG∥AB,求DG的长;
(3)连接DE,是否存在常数k,使![]() 成立?若存在,请求出k的值;若不存在,请说明理由;
成立?若存在,请求出k的值;若不存在,请说明理由;
(4)当点G在AD的右侧时,请直接写出△ADG面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,AE平分∠DAC,AE交CD于点F,CE⊥AE,垂足为点E,EG⊥CD,垂足为点G,点H在边BC上,BH=DF,连接AH、FH,FH与AC交于点M.下面结论:①FH=2BH;②AC⊥FH;③DF=1;④ EG2=FGDG.其中正确的个数为( )
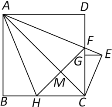
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠ACB=90°,AC=BC,D是AB上的一个动点(不与点A,B重合),连接CD,将CD绕点C顺时针旋转90°得到CE,连接DE,DE与AC相交于点F,连接AE.下列结论:①△ACE≌△BCD;②若∠BCD=25°,则∠AED=65°;③DE2=2CFCA;④若AB=3![]() ,AD=2BD,则AF=
,AD=2BD,则AF=![]() .其中正确的结论是______.(填写所有正确结论的序号)
.其中正确的结论是______.(填写所有正确结论的序号)
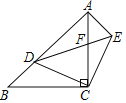
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣5与坐标轴交于A(﹣1,0),B(5,0),C(0,﹣5)三点,顶点为D.
(1)请直接写出抛物线的解析式及顶点D的坐标;
(2)连接BC与抛物线的对称轴交于点E,点P为线段BC上的一个动点(点P不与B、C两点重合),过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.
①是否存在点P,使四边形PEDF为平行四边形?若存在,求出点P的坐标;若不存在,说明理由.
②过点F作FH⊥BC于点H,求△PFH周长的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年是脱贫攻坚、全面建设小康社会关键年.为响应党的号召,蓬溪县中职校向一所希望小学赠送文具1080件,现用A、B两种不同的包装箱进行包装,已知每个B型包装箱比A型包装箱多装15件文具,单独使用B型包装箱比单独使用A型包装箱可少用12个.问B型包装箱每个可以装多少件文具?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初中阶段的函数学习中,我们经历了“确定函数的表达式——利用函数图象研究其性质——应用函数解决问题”的学习过程.在画函数图象时,我们可以通过描点或平移的方法画出一个函数的大致图象,结合上面经历的学习过程,现在来解决下面问题:
在函数![]() 中,当
中,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(1)求这个函数的表达式;
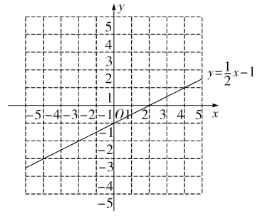
(2)在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象,并写出这个函数的一条性质;
(3)已知函数![]() 的图象如图所示,结合你所画的函数图象,直接写出不等式
的图象如图所示,结合你所画的函数图象,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com