
【题目】为了增强学生的环保意识,某校组织了一次全校2000名学生都参加的“环保知识”考试,考题共10题.考试结束后,学校团委随机抽查部分考生的考卷,对考生答题情况进行分析统计,发现所抽查的考卷中答对题量最少为6题,并且绘制了如下两幅不完整的统计图.请根据统计图提供的信息解答以下问题: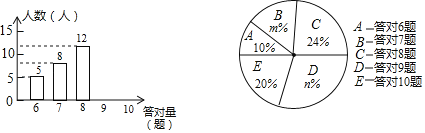
(1)本次抽查的样本容量是 ;在扇形统计图中,m= ,n= ,“答对8题”所对应扇形的圆心角为 度;
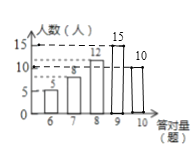
(2)将条形统计图补充完整;
(3)请根据以上调查结果,估算出该校答对不少于8题的学生人数.
【答案】(1)50,16,30,86.4;(2)补充图形见解析;(3)该校答对不少于8题的学生人数是1480人.
【解析】(1)由答对6题有有5人占10%可求出样本容量,继而根据答对7题的人数可求得m以及n,用答对8题的比例乘以360度即可求得;
(2)根据样本容量以及答对9题、10题的比例求出各自的人数,即可补全条形图;
(3)根据题意列出算式,再求出即可.
(1)5÷10%=50(人),
本次抽查的样本容量是50,
![]() =0.16=16%,1﹣10%﹣16%﹣24%﹣20%=30%,
=0.16=16%,1﹣10%﹣16%﹣24%﹣20%=30%,
即m=16,n=30,
360°×24%=86.4°,
故答案为:50,16,30,86.4;
(2)答对9题有50×30%=15人,答对10题有50×20%=10人,
如图所示:
 ;
;
(3)2000×(24%+20%+30%)=1480(人),
答:该校答对不少于8题的学生人数是1480人.


科目:初中数学 来源: 题型:
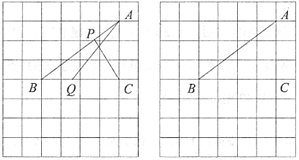
【题目】如图,在由边长都为1的小正方形组成的网格中,点![]() ,
,![]() ,
,![]() 均为格点,点
均为格点,点![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的动点,且满足
上的动点,且满足![]() .
.
(1)线段![]() 的长度等于__________;
的长度等于__________;
(2)当线段![]() 取得最小值时,请借助无刻度直尺在给定的网格中画出线段
取得最小值时,请借助无刻度直尺在给定的网格中画出线段![]() 和
和![]() ,并简要说明你是怎么画出点Q,P的:_______________________.
,并简要说明你是怎么画出点Q,P的:_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
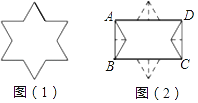
【题目】如图(1)是一个六角星的纸板,其中六个锐角都为60°,六个钝角都为120°,每条边都相等,现将该纸板按图(2)切割,并无缝隙无重叠地拼成矩形ABCD.若六角星纸板的面积为9![]() cm2,则矩形ABCD的周长为( )
cm2,则矩形ABCD的周长为( )
A.18cmB.![]() cmC.(
cmC.(![]() +6)cmD.(
+6)cmD.(![]() +6)cm
+6)cm
查看答案和解析>>
科目:初中数学 来源: 题型:
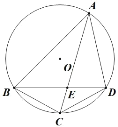
【题目】已知:如图,四边形 ABCD 内接于⊙ O ,AC 和 BD 相交于E , BC = CD = 4 , AE = 6 ,且 BE 和 DE 的长是正整数,求 BD 的 长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上的一点,连接BO交AD于点F,OE⊥OB交BC边于点E.
(1)试说明:△ABF∽△COE.
(2)如图(2),当O为AC边的中点,且![]() 时,求
时,求![]() 的值.
的值.
(3)当O为AC边的中点,![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
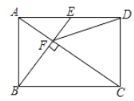
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF=![]() S△ABF.其中正确的结论有( )个
S△ABF.其中正确的结论有( )个
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在利用图象法求方程x2=![]() x+3的解x1,x2时,下面是四位同学的解法:
x+3的解x1,x2时,下面是四位同学的解法:
甲:函数y=x2﹣![]() x﹣3的图象与x轴交点的横坐标是x1,x2
x﹣3的图象与x轴交点的横坐标是x1,x2
乙:函数y=x2与y=![]() x+3的图象交点的横坐标是x1,x2
x+3的图象交点的横坐标是x1,x2
丙:函数y=x2﹣3与y=![]() x的图象交点的横坐标是x1,x2
x的图象交点的横坐标是x1,x2
丁:函数y=x2+1与y=![]() x+4的图象交点的横坐标是x1,x2
x+4的图象交点的横坐标是x1,x2
你认为解法正确的同学有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx﹣3的图象与x轴交于A、B与y轴交于点C,顶点坐标为(1,﹣4)
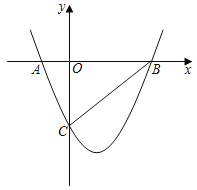
(1)求二次函数解析式;
(2)该二次函数图象上是否存在点M,使S△MAB=S△CAB,若存在,求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
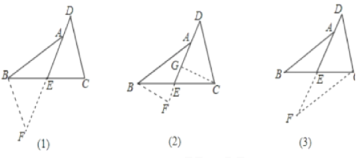
【题目】读下面的题目及分析过程,并按要求进行证明。已知:如图,E是BC的中点,点A在DB上,且
∠BAE=∠CDE,求证:AB=CD
分析:证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等。因此,要证明AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形。现给出如下三种添加辅助线的方法,请任意选择其中两种对原题进行证明。
图(1):延长DE到F使得EF=DE
图(2):作CG⊥DE于G,BF⊥DE于F交DE的延长线于F
图(3):过C点作CF∥AB交DE的延长线于F.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com