练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    若|x+1|＞2，则x的取值范围为
     
    ．
    考点：含绝对值符号的一元一次方程
    专题：
    分析：根据绝对值的意义，可得不等式，解不等式，可得答案．
    解答：解：由|x+1|＞2，得
    x+1＞2   ①，
    x+1＜-2   ②．
    解①得x＞1，
    解②得x＜-3，
    故x的取值范围为x＜-3或x＞1．
    故答案为：x＜-3或x＞1．
    点评：本题考查了含绝对值符号的一元一次方程，利用了解不等式的方法，分类讨论是解题关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，直角梯形ABCD中，AB∥CD，∠B=90°，AB=8，BC=10，CD=5，AD的中垂线MN交BC于N，求BN的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

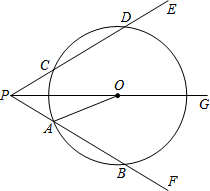    如图，射线PG平分∠EPF，O为射线PG上一点，以O为圆心，10为半径作⊙O，分别与∠EPF两边相交于A、B和C、D，连结OA，此时有OA∥PE．
    （1）求证：AP=AO；
    （2）若弦AB=12，求tan∠OPB的值；
    （3）若以图中已标明的点（即P、A、B、C、D、O）构造四边形，则能构成菱形的四个点为
     
    ，能构成等腰梯形的四个点为
     
    或
     
    或
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，AB=AD，∠ABC=∠ADC，试说明：BD的垂直平分线为直线AC．　

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    △ABC中，O是△ABC外角∠DAC平分线上任意一点，连接OB、OC．
    （1）比较AB+AC与OB+OC的关系；
    （2）当点O是（1）中△ABC的外角∠DAC的平分线的反向延长线AP上任意一点，连接OB，OC，画出图形，判断AB+AC与OB+OC之间的大小关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

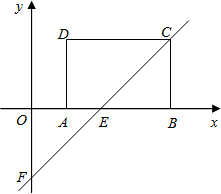    如图，在平面直角坐标系xOy中，矩形ABCD的AB边在x轴上，AB=3，AD=2，经过点C的直线y=x-2与x轴、y轴分别交于点E、F．
    （1）求：①点D的坐标；
    ②经过点D，且与直线FC平行的直线的函数表达式；
    （2）直线y=x-2上是否存在点P，使得△PDC为等腰直角三角形？若存在，求出点P 的坐标；若不存在，请说明理由．
    （3）在平面直角坐标系内确定点M，使得以点M、D、C、E为顶点的四边形是平行四边形，请直接写出点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

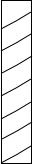    如图，有一根高为2m的圆柱形木材，它的底面周长为0.3m．为了营造喜庆的气氛，小颖想用一根彩带从圆木的底向顶均匀地缠绕7圈，一直缠到起点的正上方为止．小颖至少要准备多长的一根彩带？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

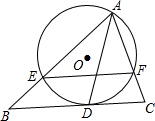    如图，直线BC与半径为2的⊙O相切于点D，A是⊙O上一点，AB交⊙O于点E，AC交⊙O于点F，BC∥EF．
    （1）求证：AD平分∠BAC；
    （2）若∠BAC=60°，求EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知正整数a，b，c满足：1＜a＜b＜c，a+b+c=111，b2=ac，则b=
     
    ．

    查看答案和解析>>

    同步练习册答案