
【题目】等腰△ABC中,AB=AC,AD⊥BC于点D,点E是AD上的一点,连接CE,将线段EC绕点E顺时针旋转一定的角度,使得点C落在了点F处,且满足∠CEF=∠CAB,连接BF
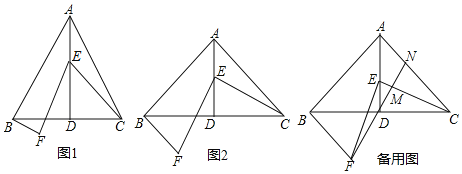
(1)如图,若∠BAC=60°,则线段AE与BF的数量关系为 ;
(2)如图,若∠BAC=90°,求证:BF=![]() AE:(写出证明过程)
AE:(写出证明过程)
(3)如图.在(2)的条件下,连接FD并延长分别交CE、CA于点M,N,BC=8,FD=![]() DE,求△DCN和△CMN的面积
DE,求△DCN和△CMN的面积
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
(1)当∠BAC=60°,根据有一个角是60°的等腰三角形是等边三角形可得△ABC,△CEF为等边三角形,再证明△ACE≌△BCF,从而得到AE=BF,(2)当∠BAC=90°时,可知△ABC,△CEF是等腰直角三角形,可证△ACE∽△BCF,利用对应边成比例,结论可证,(3)过点F作FG⊥BC于G,连接GE,由(2)可得△BGF是等腰直角三角形,进而可证FD=![]() DG,Rt△DGF中,利用勾股定理可得BF=3
DG,Rt△DGF中,利用勾股定理可得BF=3![]() ,由三角形全等可得CN=3
,由三角形全等可得CN=3![]() ,又AN=
,又AN=![]() ,则△DCN的面积=
,则△DCN的面积=![]() ×△ACD的面积=
×△ACD的面积=![]() ×8=6,过N作NH∥AD,交CE于H,由平行线分线段成比例,可得
×8=6,过N作NH∥AD,交CE于H,由平行线分线段成比例,可得![]() ,
,![]() ,则△CMN的面积=
,则△CMN的面积=![]() ×△DCN的面积=
×△DCN的面积=![]() ×6=
×6=![]() .
.
解:(1)AE=BF,理由如下,
连接CF,
当∠BAC=60°时,由AB=AC,可得△ABC是等边三角形,
∵∠CEF=∠CAB=60°,CE=FE,
∴△CEF是等边三角形,
∴∠ACB=∠ECF=60°,
∴∠ACE=∠BCF,
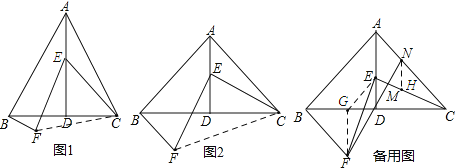
在△ACE和△BCF中
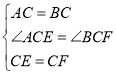 ,
,
∴△ACE≌△BCF(SAS),
∴AE=BF,
(2)连接CF,
当∠BAC=90°时,由AB=AC,可得△ABC是等腰直角三角形,
∴![]() ,
,
∵∠CEF=∠CAB=90°,CE=FE,
∴△CEF是等腰直角三角形,
∴![]() ,且∠ACB=∠ECF=45°,
,且∠ACB=∠ECF=45°,
∴![]() ,∠ACE=∠BCF,
,∠ACE=∠BCF,
∴△ACE∽△BCF,
∴![]() =
=![]() ,
,
即BF=![]() AE;
AE;
(3)过点F作FG⊥BC于G,连接GE,
由(2)可得∠FBC=∠EAC=45°,
∴△BGF是等腰直角三角形,
∴BG=FG,且BF=![]() BG,
BG,
又∵BF=![]() AE,
AE,
∴BG=AE,
∵等腰直角三角形ABC中,AD=BD=![]() BC=4,
BC=4,
∴DG=DE,
∵FD=![]() DE,
DE,
∴FD=![]() DG,
DG,
设DG=x,则GF=GB=4﹣x,DF=![]() x,
x,
∴Rt△DGF中,x2+(4﹣x)2=(![]() x)2,
x)2,
解得x1=1,x2=﹣![]() (舍去),
(舍去),
∴DG=DE=1,
∴AD=BG=FG=4﹣1=3,
∴BF=![]() =3
=3![]() ,
,
由∠FBC=∠ACD=45°,BD=CD,∠BDF=∠CDN,可得△BDF≌△CDN(ASA),
∴BF=CN=3![]() ,
,
∵Rt△ACD中,AC=![]() =4
=4![]() ,
,
∴AN=![]() ,
,
∴△DCN的面积=![]() ×△ACD的面积=
×△ACD的面积=![]() ×8=6,
×8=6,
过N作NH∥AD,交CE于H,
∴△CNH∽△CAE,
∴![]() ,即
,即![]() ,
,
∴NH=![]() ,
,
由NH∥AD,可得![]() ,即
,即![]() ,
,
∴△CMN的面积=![]() ×△DCN的面积=
×△DCN的面积=![]() ×6=
×6=![]() .
.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
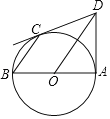
【题目】已知:如图,AB是⊙O的直径,直线DC,DA分别切⊙O于点C,点A,连结BC,OD.
(1)求证:BC∥OD.
(2)若∠ODC=36°,AB=6,求出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
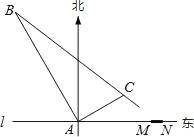
【题目】在东西方向的海岸线l上有一长为1km的码头MN(如图),在码头西端M的正西19.5km处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距![]() km的C处.
km的C处.
(1)求该轮船航行的速度(保留精确结果);
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
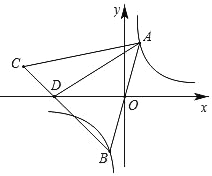
【题目】如图,已知点A是反比例函数y=![]() 的图象在第一象限上的动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC使点C落在第二象限,且边BC交x轴于点D,若△ACD与△ABD的面积之比为1:2,则点C的坐标为__.
的图象在第一象限上的动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC使点C落在第二象限,且边BC交x轴于点D,若△ACD与△ABD的面积之比为1:2,则点C的坐标为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某家庭2018年每月交通费支出的条形统计图,若该家庭2018年月交通费平均支出为a元,则下列结论中正确的是( )
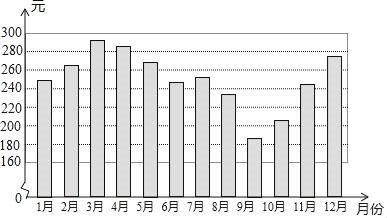
A. 200≤a≤220B. 220≤a≤240C. 240≤a≤260D. 260≤a≤280
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(1)求证:该抛物线与x轴总有交点;
(2)若该抛物线与x轴有一个交点的横坐标大于3且小于5,求m的取值范围;
(3)设抛物线![]() 与
与![]() 轴交于点M,若抛物线与x轴的一个交点关于直线
轴交于点M,若抛物线与x轴的一个交点关于直线![]() 的对称点恰好是点M,求
的对称点恰好是点M,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为等边三角形,点E为△ABC内部一点,△ABE绕点B顺时针旋转60°得到△CBD,且A、D、E三点在同一直线上,AD与BC交于点F,则以下结论中:①△BED为等边三角形;②△BED与△ABC的相似比始终不变;③△BDE∽△ADB;④当∠BAE=45°时, ![]() 其中正确的有_____(填写序号即可).
其中正确的有_____(填写序号即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
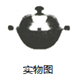
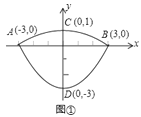
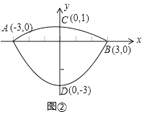
【题目】我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形,不妨简称为“锅线”,锅口直径为![]() ,锅深
,锅深![]() ,锅盖高
,锅盖高![]() (锅口直径与锅盖直径视为相同),建立直角坐标系如图①所示(图②是备用图),如果把锅纵断面的抛物线记为
(锅口直径与锅盖直径视为相同),建立直角坐标系如图①所示(图②是备用图),如果把锅纵断面的抛物线记为![]() ,把锅盖纵断面的抛物线记为
,把锅盖纵断面的抛物线记为![]() .
.
![]() 求
求![]() 和
和![]() 的解析式;
的解析式;
![]() 如果炒菜锅时的水位高度是
如果炒菜锅时的水位高度是![]() ,求此时水面的直径;
,求此时水面的直径;
![]() 如果将一个底面直径为
如果将一个底面直径为![]() ,高度为
,高度为![]() 的圆柱形器皿放入炒菜锅内蒸食物,锅盖能否正常盖上?请说明理由.
的圆柱形器皿放入炒菜锅内蒸食物,锅盖能否正常盖上?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com