
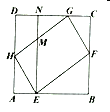
【题目】如图,平行四边形![]() 的四个顶点分别在正方形
的四个顶点分别在正方形![]() 的四条边上.
的四条边上.![]() ,分别交
,分别交![]() ,
,![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() ,且
,且![]() .要求得平行四边形
.要求得平行四边形![]() 的面积,只需知道一条线段的长度.这条线段可以是( )
的面积,只需知道一条线段的长度.这条线段可以是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
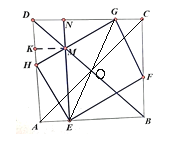
根据图形证明△AOE≌△COG,作KM⊥AD,证明四边形DKMN为正方形,再证明Rt△AEH≌Rt△CGF,Rt△DHG≌Rt△BFE,设正方形![]() 边长为a,CG=MN=x,根据正方形的性质列出平行四边形
边长为a,CG=MN=x,根据正方形的性质列出平行四边形![]() 的面积的代数式,再化简整理,即可判断.
的面积的代数式,再化简整理,即可判断.
连接AC,EG,交于O点,
∵四边形![]() 是平行四边形,四边形
是平行四边形,四边形![]() 是正方形,
是正方形,
∴GO=EO,AO=CO,
又∠AOE=∠COG
∴△AOE≌△COG,
∴GC=AE,
∵NE∥AD,
∴四边形AEND为矩形,
∴AE=DN,
∴DN=GC=MN
作KM⊥AD,
∴四边形DKMN为正方形,
在Rt△AEH和Rt△CGF中,
![]()
∴Rt△AEH≌Rt△CGF,
∴AH=CF,
∵AD-AH=BC-CF
∴DH=BF,
同理Rt△DHG≌Rt△BFE,
设CG=MN=x,
设正方形![]() 边长为a
边长为a
则S△HDG=![]() DH×x+
DH×x+![]() DG×x=S△FBE
DG×x=S△FBE
S△HAE=![]() AH×x =S△GCF
AH×x =S△GCF
S平行四边形EFGH=a2-2S△HDG-2S△HAE= a2-(DH+DG+AH)×x,
∵DG=a-x
∴S平行四边形EFGH= a2-(a+a-x)×x= a2-2ax+x2= (a-x)2
故只需要知道a-x就可以求出面积
BE=a-x,故选C.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() 与
与![]() 轴左侧抛物线交于点
轴左侧抛物线交于点![]() ,直线
,直线![]() 与
与![]() 轴右侧抛物线交于点
轴右侧抛物线交于点![]() .
.
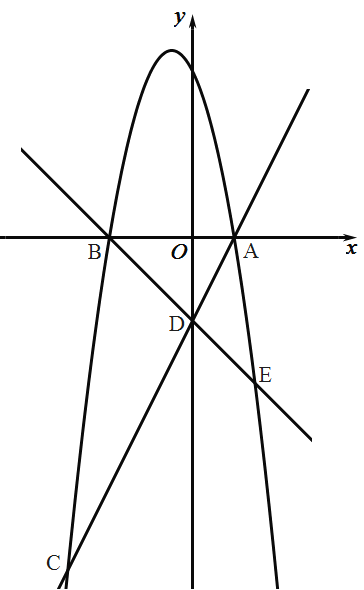
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 上方抛物线上一动点,求
上方抛物线上一动点,求![]() 面积的最大值;
面积的最大值;
(3)点![]() 是抛物线上一动点,点
是抛物线上一动点,点![]() 是抛物线对称轴上一动点,请直接写出以点
是抛物线对称轴上一动点,请直接写出以点![]() 为顶点的四边形是平行四边形时点
为顶点的四边形是平行四边形时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
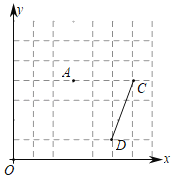
【题目】如图,在边长为1的正方形网格中,点A(3,4),⊙A的半径为![]() .
.
(1)请在网格中画出⊙A;
(2)请标出⊙A上的三个相邻的格点B1、B2、B3,连接B1B3,则由![]() 和弦B1B3围成的弓形面积为 ;
和弦B1B3围成的弓形面积为 ;
(3)线段CD,点C(6,4)、D(5,1),在⊙A上有一点M,使△CDM的面积最大,请找到此时的点M(保留必要辅助格点N).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB为直径,AC=5,AB=10,
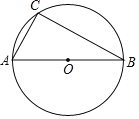
(1)作以AC为底边的圆内接等腰△ACD;(要求:尺规作图,不写作法,保留作图痕迹)
(2)求弦AC所对的圆周角。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (
(![]() ,
,![]() ,
,![]() 为常数,且
为常数,且![]() )中的
)中的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
以下结论:
①二次函数![]() 有最小值为
有最小值为![]() ;
;
②当![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
③二次函数![]() 的图象与
的图象与![]() 轴只有一个交点;
轴只有一个交点;
④当![]() 时,
时,![]() .
.
其中正确的结论有( )个
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
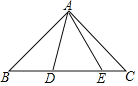
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°
(1)若BD=2,CE=4,则DE=_____.
(2)若∠AEB=75°,则线段BD与CE的数量关系是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
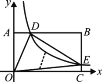
【题目】如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数![]() (x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k的值是( )
(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k的值是( )
A.![]() B.
B.![]() C.
C.![]() D.12
D.12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com