
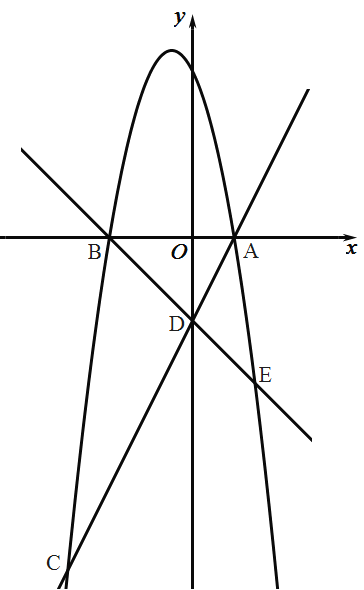
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() 与
与![]() 轴左侧抛物线交于点
轴左侧抛物线交于点![]() ,直线
,直线![]() 与
与![]() 轴右侧抛物线交于点
轴右侧抛物线交于点![]() .
.
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 上方抛物线上一动点,求
上方抛物线上一动点,求![]() 面积的最大值;
面积的最大值;
(3)点![]() 是抛物线上一动点,点
是抛物线上一动点,点![]() 是抛物线对称轴上一动点,请直接写出以点
是抛物线对称轴上一动点,请直接写出以点![]() 为顶点的四边形是平行四边形时点
为顶点的四边形是平行四边形时点![]() 的坐标.
的坐标.
【答案】(1) ![]() ;(2)当
;(2)当![]() 时,
时,![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)直接利用待定系数法,即可求出解析式;
(2)先求出点C的坐标,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,设P
,设P![]() ,则
,则![]() ,则得到线段PQ的长度,然后利用三角形面积公式,即可求出答案;
,则得到线段PQ的长度,然后利用三角形面积公式,即可求出答案;
(3)先求出直线BD,然后得到点E的坐标,由以点![]() 为顶点的四边形是平行四边形,设点M为(m,
为顶点的四边形是平行四边形,设点M为(m,![]() ),则可分为三种情况进行①当CN与ME为对角线时;②当CE与MN为对角线时;③当EN与CM为对角线时;由平行四边形对角线互相平分,即可得到m的值,然后求出点M的坐标.
),则可分为三种情况进行①当CN与ME为对角线时;②当CE与MN为对角线时;③当EN与CM为对角线时;由平行四边形对角线互相平分,即可得到m的值,然后求出点M的坐标.
解:(1)把![]() 代入中得
代入中得![]() ,
,
![]()
解得![]() ,
,
![]() 抛物线的解析式为:
抛物线的解析式为:![]() .
.
(2)由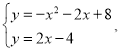
得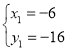 ,
, ,
,
![]() .
.
过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,
,
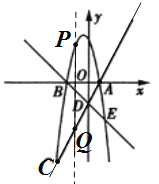
设![]() ,则
,则![]() ,
,
![]() ,
,
![]()
![]()
![]() .
.
![]() 当
当![]() 时,
时,![]() ;
;
∴![]() 面积的最大值为64.
面积的最大值为64.
(3)∵直线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
∴点D的坐标为:(0,![]() ),
),
∵点B为(![]() ),
),
∴直线BD的方程为:![]() ;
;
联合抛物线与直线BD,得:
![]() ,
,
解得: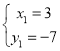 或
或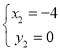 (为点B),
(为点B),
∴点E的坐标为:(3,![]() );
);
∵抛物线![]() 的对称轴为:
的对称轴为:![]() ,
,
∴点N的横坐标为![]() ;
;
∵以点![]() 为顶点的四边形是平行四边形,且点C(
为顶点的四边形是平行四边形,且点C(![]() ),点E(3,
),点E(3,![]() ),
),
设点M为(m,![]() ),则可分为三种情况进行
),则可分为三种情况进行
①当CN与ME为对角线时,由平行四边形对角线互相平分,
∴![]() ,
,
解得:![]() ;
;
∴点M的纵坐标为:![]() ,
,
∴点M的坐标为:(![]() );
);
②当CE与MN为对角线时,由平行四边形对角线互相平分,
∴![]() ,
,
解得:![]() ,
,
∴点M的纵坐标为:![]() ,
,
∴点M的坐标为:(![]() );
);
③当EN与CM为对角线时,由平行四边形对角线互相平分,
∴![]() ,
,
解得:![]() ,
,
∴点M的纵坐标为:![]() ;
;
∴点M的坐标为:(![]() );
);
综合上述,点![]() 的坐标为:
的坐标为:![]() 或
或![]() .
.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
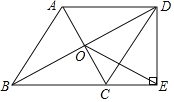
【题目】如图,在四边形ABCD中,AD∥BC,AB=BC,对角线AC、BD交于点O,BD平分∠ABC,过点D作DE⊥BC,交BC的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若DC=2![]() ,AC=4,求OE的长.
,AC=4,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙0的直径,点C在⊙0上,D是![]() 中点,若∠BAC=70°,求∠C.
中点,若∠BAC=70°,求∠C.
下面是小雯的解法,请帮他补充完整:
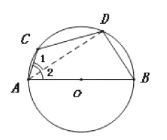
解:在⊙0中,
∵D是![]() 的中点
的中点
∴BD=CD.
∴∠1=∠2( )(填推理的依据).
∵∠BAC=70°,
∴∠2=35°.
∵AB是⊙0的直径,
∴∠ADB=90°( )(填推理的依据).
∴∠B=90°-∠2=55°.
∵A、B、C、D四个点都在⊙0上,
∴∠C+∠B=180°( )(填推理的依据).
∴∠C=180°-∠B= (填计算结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(2,y1),B(﹣3,y2),C(﹣5,y3)三个点都在反比例函数![]() 的图象上,比较y1,y2,y3的大小,则下列各式正确的是( )
的图象上,比较y1,y2,y3的大小,则下列各式正确的是( )
A.y1<y2<y3B.y2<y3<y1C.y1<y3<y2D.y3<y2<y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A、B和点C、D,先用卷尺量得AB=160m,CD=40m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).
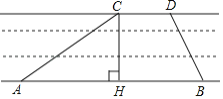
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AD、BD分别是△ABC的内角∠BAC、∠ABC的平分线,过点A作AE⊥AD,交BD的延长线于点E.
(1)求证:∠E=![]() ∠C;
∠C;
(2)如图2,如果AE=AB,且BD:DE=2:3,求cos∠ABC的值;
(3)如果∠ABC是锐角,且△ABC与△ADE相似,求∠ABC的度数.
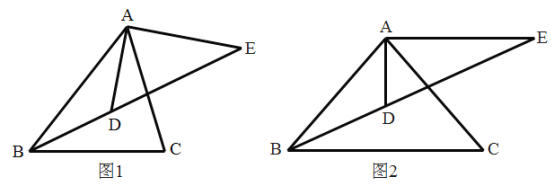
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.三角形的外心一定在三角形的外部B.三角形的内心到三个顶点的距离相等
C.外心和内心重合的三角形一定是等边三角形D.直角三角形内心到两锐角顶点连线的夹角为125°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形![]() 的四个顶点分别在正方形
的四个顶点分别在正方形![]() 的四条边上.
的四条边上.![]() ,分别交
,分别交![]() ,
,![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() ,且
,且![]() .要求得平行四边形
.要求得平行四边形![]() 的面积,只需知道一条线段的长度.这条线段可以是( )
的面积,只需知道一条线段的长度.这条线段可以是( )
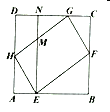
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com