
【题目】如图,在平行四边形ABCD中,点O是边BC的中点,连接AO并延长,交DC延长线于点E,连接AC,BE.
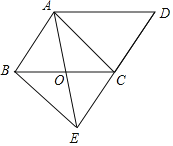
(1)求证:四边形ABEC是平行四边形;
(2)当∠D=50°,∠AOC=100°时,判断四边形ABEC的形状,并说明理由.
【答案】(1)见解析;(2)四边形ABEC是矩形,理由见解析.
【解析】
(1)由平行四边形的性质可得AB∥CD,可得∠BAO=∠CEO,∠ABO=∠ECO,由“AAS”可证△ABO≌△ECO,可得AO=EO,即可证四边形ABEC是平行四边形;
(2)由平行四边形的性质和三角形外角性质可证AO=BO,可得AE=BC,即可得四边形ABEC是矩形.
证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAO=∠CEO,∠ABO=∠ECO,
∵点O是边BC的中点,
∴BO=CO,且∠BAO=∠CEO,∠ABO=∠ECO,
∴△ABO≌△ECO(AAS),
∴AO=EO,且BO=CO,
∴四边形ABEC是平行四边形;
(2)四边形ABEC是矩形,
理由如下:∵四边形ABCD是平行四边形,
∴∠ABC=∠D=50°,
∵∠AOC=∠ABC+∠BAO=100°,
∴∠ABC=∠BAO=50°,
∴AO=BO,
∴AE=BC,
∴ABEC是矩形.


科目:初中数学 来源: 题型:
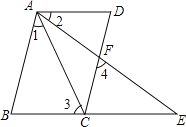
【题目】如图,已知AB∥CD,∠1=∠2,∠3=∠4,则AD∥BE.完成下列推理过程:
证明:∵AB∥CD(已知)
∴∠4= ( )
∵∠3=∠4(已知)
∴∠3= ( )
∵∠1=∠2(已知)
∴∠CAE+∠1=∠CAE+∠2
即∠ =∠
∴∠3=
∴AD∥BE( )
查看答案和解析>>
科目:初中数学 来源: 题型:
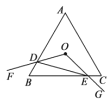
【题目】如图,等边三角形![]() 的边长为4,点
的边长为4,点![]() 是△
是△![]() 的中心,
的中心,![]() .绕点
.绕点![]() 旋转
旋转![]() ,分别交线段
,分别交线段![]() 于
于![]() 两点,连接
两点,连接![]() ,给出下列四个结论:①
,给出下列四个结论:①![]() ;②
;②![]() ;③四边形
;③四边形![]() 的面积始终等于
的面积始终等于![]() ;④△
;④△![]() 周长的最小值为6,上述结论中正确的个数是( )
周长的最小值为6,上述结论中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
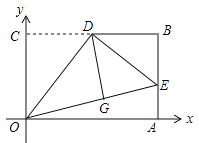
【题目】如图,在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在x轴和y轴上,OC=3,OA=![]() ,D是BC的中点,将△OCD沿直线OD折叠后得到△OGD,延长OG交AB于点E,连接DE,则点G的坐标为 .
,D是BC的中点,将△OCD沿直线OD折叠后得到△OGD,延长OG交AB于点E,连接DE,则点G的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
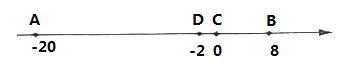
【题目】如图,在数轴上点![]() 对应的数为
对应的数为![]() ,点
,点![]() 对应的数为8,点
对应的数为8,点![]() 对应的数为
对应的数为![]() ,
,![]() 为原点.
为原点.
(1)![]() 两点的距离是_____;
两点的距离是_____;
(2)若点![]() 以每秒5个单位长度的速度沿数轴正方向运动,则2秒时
以每秒5个单位长度的速度沿数轴正方向运动,则2秒时![]() ,
,![]() 两点的距离是_____;
两点的距离是_____;
(3)若点![]() 都以每秒4个单位长度的速度沿数轴正方向运动,而点
都以每秒4个单位长度的速度沿数轴正方向运动,而点![]() 不动,
不动,![]() 秒时,
秒时,![]() 中有一点是三点所在线段的中点,求
中有一点是三点所在线段的中点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
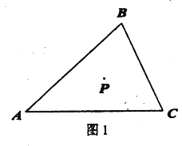
【题目】P是三角形![]() 内一点,射线PD//AC ,射线PB//AB .
内一点,射线PD//AC ,射线PB//AB .
(1)当点D,E分别在AB,BC 上时,
①补全图1:
②猜想![]() 与
与![]() 的数量关系,并证明;,
的数量关系,并证明;,
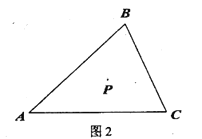
(2)当点![]() 都在线段
都在线段![]() 上时,请先画出图形,想一想你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由
上时,请先画出图形,想一想你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com