Question

1．已知AB是⊙O的直径，P为AB延长线上的任意一点，过点P作⊙O的切线，切点为C，∠APC的平分线PD与AC交于点D．
（1）如图①，若∠CPA恰好等于30°，求∠CDP的度数；
（2）如图②，若∠CPA不等于30°时，①中的结论是否仍然成立？请说明理由．

Answer 1

分析 （1）利用切线的性质得出∠OCP=90°，进而利用∠CPA=30°，得出∠COP的度数，进而结合角平分线的性质得出∠APD，再利用∠CDP=∠A+∠APD求出答案；
（2）利用切线的性质得出∠OCP=90°，结合角平分线的性质得出∠APC=2∠APD，结合∠COP=2∠A，得出2（∠A+∠APD）=90°，进而求出答案．

解答 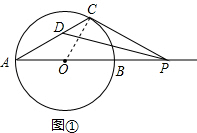解：（1）如图①，连接OC，
∵直线PC是⊙O的切线，
∴OC⊥PC，则∠OCP=90°，
∵∠CPA=30°，
∴∠COP=90°-30°=60°，
∵OA=OC，
∴∠A=∠ACO=30°，
∵PD平分∠APC，
∴∠APD=$\frac{1}{2}$×30°=15°，
∴∠CDP=∠A+∠APD=30°+15°=45°，
即∠CDP的度数为：45°；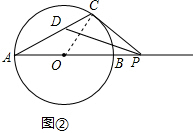

（2）∠CDP的大小不发生变化，
理由：如图②，连接CO，
∵PC是⊙O的切线，
∴∠OCP=90°，
∵PD是∠CPA的平分线，
∴∠APC=2∠APD，
∵OA=OC，
∴∠A=∠ACO，
∴∠COP=2∠A，
∴∠COP+∠APC=90°，即2（∠A+∠APD）=90°，
∴∠CDP=∠A+∠APD=45°，
故∠CDP的大小不发生变化．

点评 此题主要考查了切线的性质以及角平分线的性质，正确得出2（∠A+∠APD）=90°是解题关键．