
����Ŀ���Ķ�������ϣ�
С����������һ�����⣺
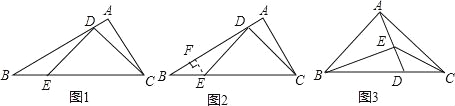
��ͼ1����ABC�У���A=90�㣬��B=30�㣬��D��E�ֱ���AB��BC�ϣ�����CDE=90�㣮��BE=2ADʱ��ͼ1���Ƿ������CD��ȵ��߶Σ������ڣ����ҳ�������֤�����������ڣ�˵�����ɣ�
С��ͨ��̽�����֣�����E��AB�Ĵ���EF������ΪF���ܵõ�һ��ȫ�������Σ���ͼ2�����Ӷ���������⣮
��ش�
��1��С�����ֵ���CD��ȵ��߶��� ��
��2��֤��С�����ֵĽ��ۣ�
�ο�С��˼������ķ����������������⣺
��3����ͼ3����ABC�У�AB=AC����BAC=90�㣬��D��BC�ϣ�BD=2DC����E��AD�ϣ�����BEC=135�㣬��![]() ��ֵ��
��ֵ��
���𰸡���1��DE��2��֤����������3��![]()
��������
�����������1��ֱ��д���𰸣�
��2�����жϳ���ADC=ADC=��FEDFED�����жϳ�FE=AD�������жϳ���FEDFED�ա�ADCADC���ɣ�
��3�����жϳ���FBE=FBE=��GECGEC�������ó���BFEBFE�ס�EGC���ó�![]() �����жϳ�FE=2EG�����ɵó����ۣ�
�����жϳ�FE=2EG�����ɵó����ۣ�
�����������1��DE��
�ʴ�Ϊ��DE��
��2��֤������EF��AB������ΪF��
����BFE=��DFE=90���T��A�T��CDE��
�ߡ�ADC+��CDE=��ADE=��DFE+��FED��
���ADC=��FED��
�ߡ�BFE=90�㣬��B=30�㣬
��BE=2FE��
��BE=2AD��
��FE=AD��
����FED����ADC��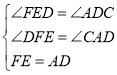
���FED�ա�ADC��
��DE=CD
��3����ͼ3��
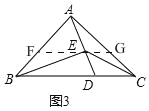
����E��BC��ƽ���ߣ���AB��AC�ֱ��ཻ�ڵ�F��G��
��AB=AC����BAC=90�㣬
���ABC=��ACB=45�㣮
��FG��BC��
���AFG=��ABC=��ACB=��AGF=45�㣬��BFE=135��=��EGC��
��AF=AG��BF=GC��
�ߡ�GEC+��CEB=��GEB=��EFB+��FBE��
���FBE=��GEC
���BFE�ס�EGC��
��![]() ��
��
��FG��BC��
���AFE�ס�ABD����AFG�ס�ADC��
��![]() ��
��![]()
��![]()
��BD=2DC��
��FE=2EG��
��![]() ��
��
��![]() ��
��
��![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
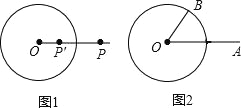
����Ŀ����ͼ1����O�İ뾶Ϊr��r��0��������P��������OP�ϣ�����OP��OP=r2����Ƶ�P���ǵ�P������O�ġ����ݵ㡱��
��ͼ2����O�İ뾶Ϊ4����B����O�ϣ���BOA=60�㣬OA=8������A�䣬B��ֱ��ǵ�A��B������O�ķ��ݵ㣬��A��B��ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��O��B������ͬһֱ���ϣ�OE��OD�ֱ�ƽ�֡�AOC����BOC�� 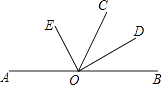
��1�����EOD�Ķ�����
��2������AOE=50�㣬���BOC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и���������ȷ���ǣ�������
A. 3x+3y=6xy B. x+x=x2
C. ��9y2+16y2=7 D. 9a2b��9a2b=0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�AB=AC����D��ֱ��BC��һ�㣨����B��C�غϣ�����ADΪһ����AD���Ҳ�����ADE��ʹAD=AE����DAE=��BAC������CE��
��1����ͼ1������D���߶�BC�ϣ������BAC=90�������BCE=�����ȣ�
��2�����BAC=������BCE=�£�
����ͼ2������D���߶�BC���ƶ�����������֮����������������ϵ����˵�����ɣ�
�ڵ���D��ֱ��BC���ƶ�����������֮����������������ϵ����ֱ��д����Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�κ���y=2x��m��ͼ����x���ཻ�ڵ�A����3��0������m��ֵΪ��������
A.��3B.6C.��6D.6��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������y=��k-3��x��ͼ��һ�������ޣ���ôk��ȡֵ��Χ�ǣ�������
A. k��0 B. k��3 C. k��0 D. k��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����a��b��Ϊ�෴����x��y��Ϊ��������2014a��2015xy+2014b��ֵ�� ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com