
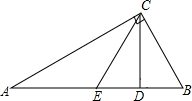
 已知:如图,在△ABC中,∠A=30°,∠ACB=90°,E、D分别是AB、EB中点.求证:CD⊥AB.
已知:如图,在△ABC中,∠A=30°,∠ACB=90°,E、D分别是AB、EB中点.求证:CD⊥AB.分析 根据直角三角形中,30°所对的直角边是斜边的一半、直角三角形斜边上的中线等于斜边的一半得到CE=CB,根据等腰三角形的性质证明即可.
解答 证明:∵∠A=30°,∠ACB=90°
∴BC=$\frac{1}{2}$AB(直角三角形中,30°所对的直角边是斜边的一半)
又∵E是AB中点
∴CE=$\frac{1}{2}$AB(直角三角形斜边上的中线等于斜边的一半),
∴CE=CB,
又∵D是EB中点,
∴CD⊥AB(等腰三角形三线合一),
故答案为:BC;直角三角形中,30°所对的直角边是斜边的一半;CE;$\frac{1}{2}$AB;直角三角形斜边上的中线等于斜边的一半;CE;CB;等腰三角形三线合一.
点评 本题考查的是直角三角形的性质和等腰三角形的性质,掌握直角三角形中,30°所对的直角边是斜边的一半、直角三角形斜边上的中线等于斜边的一半是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
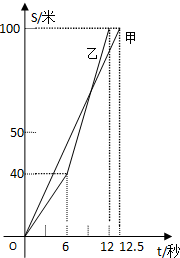 甲、乙两同学在一次百米赛跑中,路程S(米)与时间t(秒)之间的关系如图所示.根据图象回答下列问题:
甲、乙两同学在一次百米赛跑中,路程S(米)与时间t(秒)之间的关系如图所示.根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星 期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增 减 | -5 | +10 | -3 | +4 | +6 | -8 | -6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
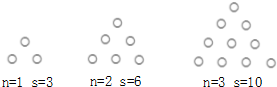 如图所示每个图形是由若干个花盆组成的三角形的图案,每条边(包括顶点)有n(n>1)盆花,每个图案共有s盆花,则s与n之间的关系式为s=$\frac{(n+1)(n+2)}{2}$.
如图所示每个图形是由若干个花盆组成的三角形的图案,每条边(包括顶点)有n(n>1)盆花,每个图案共有s盆花,则s与n之间的关系式为s=$\frac{(n+1)(n+2)}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com