
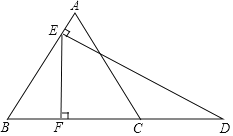
【题目】如图,△ABC是等边三角形,D是BC延长线上一点,DE⊥AB于点E,EF⊥BC于点F.若CD=3AE,CF=6,则AC的长为_____.
科目:初中数学 来源: 题型:
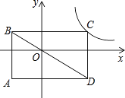
【题目】如图,矩形ABCD的对角线经过原点,各边分别平行于坐标轴,点C在反比例函数y=![]() 的图象上.若点A的坐标为(﹣2,﹣3),则k的值为________.
的图象上.若点A的坐标为(﹣2,﹣3),则k的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电信公司给用户提供了两种手机上网计费方式:
方式![]() :以每分钟0.1元的价格按上网时间计费;
:以每分钟0.1元的价格按上网时间计费;
方式![]() :除收月租费20元外,再以每分钟0.06元的价格按上网时间计费.
:除收月租费20元外,再以每分钟0.06元的价格按上网时间计费.
假设用户甲一个月手机上网的时间共有![]() 分钟,上网的费用为
分钟,上网的费用为![]() 元.
元.
(1)分别写出用户甲按![]() 两种方式计费的上网费
两种方式计费的上网费![]() 元与上网时间分钟
元与上网时间分钟![]() 之间的函数关系式;
之间的函数关系式;
(2)如果该用户每月通话时间400分钟,选择哪种计费方式更合算?
(3)如果该用户每月上网费为80元,选择哪种计费方式更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
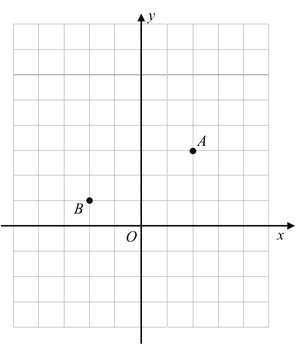
【题目】如图,在平面直角坐标系中,已知点A(2,3),点B(﹣2,1).
(1)请运用所学数学知识构造图形求出AB的长;
(2)若Rt△ABC中,点C在坐标轴上,请在备用图1中画出图形,找出所有的点C后不用计算写出你能写出的点C的坐标;
(3)在x轴上是否存在点P,使PA=PB且PA+PB最小?若存在,就求出点P的坐标;若不存在,请简要说明理由(在备用图2中画出示意图).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在阳光体育活动时间,小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.
(1)如果确定小亮打第一场,再从其余三人中随机选取一人打第一场,求恰好选中大刚的概率;
(2)如果确定小亮做裁判,用“手心、手背”的方法决定其余三人哪两人打第一场.游戏规则是:三人同时伸“手心、手背”中的一种手势,如果恰好有两人伸出的手势相同,那么这两人上场,否则重新开始,这三人伸出“手心”或“手背”都是随机的,请用画树状图的方法求小莹和小芳打第一场的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距20千米,甲、乙两人都从A地去B地,图中射线l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系.
下列说法:
①乙晚出发1小时;
②乙出发3小时后追上甲;
③甲的速度是4千米/小时,乙的速度是6千米/小时;
④乙先到达B地.其中正确的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
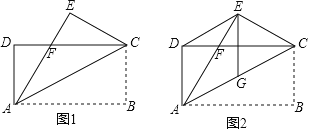
【题目】如图1,已知矩形ABCD,连接AC,将△ABC沿AC所在直线翻折,得到△AEC,AE交CD于点F.
(1)求证:DF=EF;
(2)如图2,若∠BAC=30°,点G是AC的中点,连接DE,EG,求证:四边形ADEG是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射手在一次射击中,射中![]() 环、
环、![]() 环、
环、![]() 环的概率分别是
环的概率分别是![]() 、
、![]() 、
、![]() ,那么,这个射手在这次射击中,射中
,那么,这个射手在这次射击中,射中![]() 环或
环或![]() 环的概率为________;不够
环的概率为________;不够![]() 环的概率为________.
环的概率为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com