
【题目】某电信公司给用户提供了两种手机上网计费方式:
方式![]() :以每分钟0.1元的价格按上网时间计费;
:以每分钟0.1元的价格按上网时间计费;
方式![]() :除收月租费20元外,再以每分钟0.06元的价格按上网时间计费.
:除收月租费20元外,再以每分钟0.06元的价格按上网时间计费.
假设用户甲一个月手机上网的时间共有![]() 分钟,上网的费用为
分钟,上网的费用为![]() 元.
元.
(1)分别写出用户甲按![]() 两种方式计费的上网费
两种方式计费的上网费![]() 元与上网时间分钟
元与上网时间分钟![]() 之间的函数关系式;
之间的函数关系式;
(2)如果该用户每月通话时间400分钟,选择哪种计费方式更合算?
(3)如果该用户每月上网费为80元,选择哪种计费方式更合算?
【答案】(1)方式A:![]() ;方式B:
;方式B:![]() ;(2)该用户每月通话时间400分钟,选择方式A省钱;(3)该用户每月上网费为80元,选择方式B上网时间更长,更划算.
;(2)该用户每月通话时间400分钟,选择方式A省钱;(3)该用户每月上网费为80元,选择方式B上网时间更长,更划算.
【解析】
(1)方式A的费用=0.1×上网时间;方式B的费用=月基费+0.06×上网时间;
(2)联立方程组求解两个函数图像的交点坐标,根据图像进行回答即可;
(3)由(2)中的图像中,根据图像进行回答即可.
解:(1)依题意得:方式A:![]() ,
,
方式B:![]() ,
,
(2)两个函数的图象如图所示.

∵![]()
∴![]()
∴两图象交于点P(500,50).
由图象可知:该用户每月通话时间400分钟,选择方式A省钱;
(3)由(2)中图象可知:该用户每月上网费为80元,选择方式B上网时间更长,更划算.


科目:初中数学 来源: 题型:
【题目】(1)如图1,O是等边△ABC内一点,连接OA、OB、OC,且OA=3,OB=4,OC=5,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.求:

①旋转角的度数;
②线段OD的长;
③∠BDC的度数.
(2)如图2所示,O是等腰直角△ABC(∠ABC=90°)内一点,连接OA、OB、OC,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.当OA、OB、OC满足什么条件时,∠ODC=90°?请给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
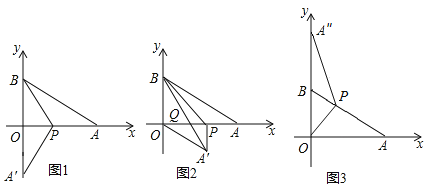
【题目】将一个直角三角形纸片![]() 放置在平面直角坐标系中,点
放置在平面直角坐标系中,点![]() .
.
(1)点![]() 为边
为边![]() 上一点(点
上一点(点![]() 不与
不与![]() 重合),沿
重合),沿![]() 将纸片折叠得
将纸片折叠得![]() 的对应点
的对应点![]() ,边
,边![]() 与
与![]() 轴交于点
轴交于点![]() .
.
①如图1,当点![]() 刚好落在
刚好落在![]() 轴上时,求点
轴上时,求点![]() 的坐标
的坐标
②如图2,当![]() 时,若线段
时,若线段![]() 在
在![]() 轴上移动得到线段
轴上移动得到线段![]() (线段
(线段![]() 平移时
平移时![]() 不动),当△A′O′Q′周长最小时,求OO′的长度.
不动),当△A′O′Q′周长最小时,求OO′的长度.
(2)如图3,若点![]() 为边
为边![]() 上一点(点
上一点(点![]() 不与
不与![]()
![]() 重合),沿
重合),沿![]() 将纸片折叠得
将纸片折叠得![]() 的对应点
的对应点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
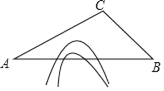
【题目】随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起.高铁大大缩短了时空距离,改变了人们的出行方式.如图,A,B两地被大山阻隔,由A地到B地需要绕行C地,若打通穿山隧道,建成A,B两地的直达高铁,可以缩短从A地到B地的路程.已知:∠CAB=30°,∠CBA=45°,AC=640公里,求隧道打通后与打通前相比,从A地到B地的路程将约缩短多少公里?(参考数据:![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
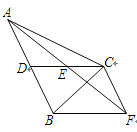
(1) 求证:CF=AD;
(2) 若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,AB=AC=BC,∠BDC=120°且BD=DC,现以D为顶点作一个60°角,使角两边分别交AB,AC边所在直线于M,N两点,连接MN,探究线段BM、MN、NC之间的关系,并加以证明.
(1)如图1,若∠MDN的两边分别交AB,AC边于M,N两点.猜想:BM+NC=MN.延长AC到点E,使CE=BM,连接DE,再证明两次三角形全等可证.请你按照该思路写出完整的证明过程;
(2)如图2,若点M、N分别是AB、CA的延长线上的一点,其它条件不变,再探究线段BM,MN,NC之间的关系,请直接写出你的猜想(不用证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
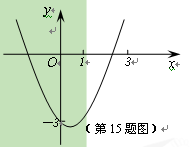
【题目】(11·湖州)如图,已知抛物线![]() 经过点(0,-3),请你确定一个
经过点(0,-3),请你确定一个
b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间。你确定的b的值是 ▲![]() 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com