
【题目】如图,矩形ABCD的对角线经过原点,各边分别平行于坐标轴,点C在反比例函数y=![]() 的图象上.若点A的坐标为(﹣2,﹣3),则k的值为________.
的图象上.若点A的坐标为(﹣2,﹣3),则k的值为________.
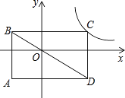
【答案】﹣1或6
【解析】
根据矩形的对角线将矩形分成面积相等的两个直角三角形,找到图中的所有矩形及相等的三角形,即可推出S四边形CEOF=S四边形HAGO,根据反比例函数比例系数的几何意义即可求出k2-5k=6,再解出k的值即可.
如图:
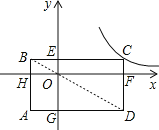
∵四边形ABCD、HBEO、OECF、GOFD为矩形,
又∵BO为四边形HBEO的对角线,OD为四边形OGDF的对角线,
∴S△BEO=S△BHO,S△OFD=S△OGD,S△CBD=S△ADB,
∴S△CBD-S△BEO-S△OFD=S△ADB-S△BHO-S△OGD,
∴S四边形CEOF=S四边形HAGO=2×3=6,
∴xy=k2-5k=6,
解得k=-1或k=6.
故答案为:-1或6.


科目:初中数学 来源: 题型:
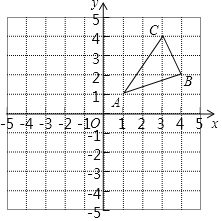
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;
(3)P为x轴上一动点,当AP+CP有最小值时,求这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直角三角形的判定
(1)有一个角是________________的三角形是直角三角形.
(2)有两个角________________的三角形是直角三角形.
(3)勾股定理的逆定理:如果三角形两边的平方和等于________________,那么这个三角形是直角三角形.
(4)如果三角形一边上的________________等于这边的一半,那么这个三角形是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个直角三角形纸片![]() 放置在平面直角坐标系中,点
放置在平面直角坐标系中,点![]() .
.
(1)点![]() 为边
为边![]() 上一点(点
上一点(点![]() 不与
不与![]() 重合),沿
重合),沿![]() 将纸片折叠得
将纸片折叠得![]() 的对应点
的对应点![]() ,边
,边![]() 与
与![]() 轴交于点
轴交于点![]() .
.
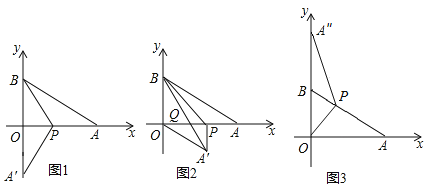
①如图1,当点![]() 刚好落在
刚好落在![]() 轴上时,求点
轴上时,求点![]() 的坐标
的坐标
②如图2,当![]() 时,若线段
时,若线段![]() 在
在![]() 轴上移动得到线段
轴上移动得到线段![]() (线段
(线段![]() 平移时
平移时![]() 不动),当△A′O′Q′周长最小时,求OO′的长度.
不动),当△A′O′Q′周长最小时,求OO′的长度.
(2)如图3,若点![]() 为边
为边![]() 上一点(点
上一点(点![]() 不与
不与![]()
![]() 重合),沿
重合),沿![]() 将纸片折叠得
将纸片折叠得![]() 的对应点
的对应点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
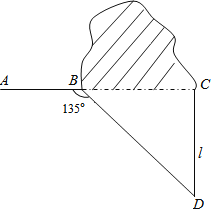
【题目】如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(![]() ≈1.414,精确到1米)
≈1.414,精确到1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
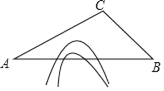
【题目】随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起.高铁大大缩短了时空距离,改变了人们的出行方式.如图,A,B两地被大山阻隔,由A地到B地需要绕行C地,若打通穿山隧道,建成A,B两地的直达高铁,可以缩短从A地到B地的路程.已知:∠CAB=30°,∠CBA=45°,AC=640公里,求隧道打通后与打通前相比,从A地到B地的路程将约缩短多少公里?(参考数据:![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
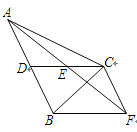
(1) 求证:CF=AD;
(2) 若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 边上一点.
边上一点.
(1)直线![]() 垂直于
垂直于![]() 于点
于点![]() 交
交![]() 于点
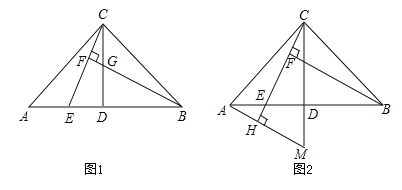
于点![]() (如图1),求证
(如图1),求证![]() ;
;
(2)直线![]() 垂直于
垂直于![]() ,垂足为
,垂足为![]() 交
交![]() 的延长线于点
的延长线于点![]() (如图2).求证:
(如图2).求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com