
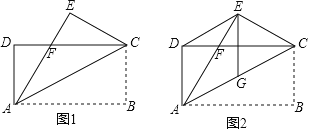
【题目】如图1,已知矩形ABCD,连接AC,将△ABC沿AC所在直线翻折,得到△AEC,AE交CD于点F.
(1)求证:DF=EF;
(2)如图2,若∠BAC=30°,点G是AC的中点,连接DE,EG,求证:四边形ADEG是菱形.
【答案】(1)证明见详解;(2)证明见详解.
【解析】
(1)根据矩形的性质得到AD=BC,∠D=∠B=90°,由折叠的性质得到∠E=∠B=90°,CE=BC.根据全等三角形的性质即可得到结论;
(2)根据折叠的性质得到∠AEC=∠B=90°,CE=BC,根据直角三角形的性质得到CE= ![]() AC,CE=AG=EG=AD,根据菱形的判定定理即可得到结论.
AC,CE=AG=EG=AD,根据菱形的判定定理即可得到结论.
解:(1)∵四边形ABCD是矩形,
∴AD=BC,∠D=∠B=90°.
∵将△ABC沿AC所在直线翻折,得到△AEC,
∴∠E=∠B=90°,CE=BC,
∴∠D=∠E,AD=CE.
∵∠AFD=∠CFE,
∴△ADF≌△CEF(AAS),
∴DF=EF;
(2)∵四边形ABCD是矩形,
∴AD=BC,∠ADC=∠B=90°.
∵将△ABC沿AC所在直线翻折,得到△AEC,
∴∠AEC=∠B=90°,CE=BC.
∵∠CAB=30°,
∴∠CAE=30°,
∴CE![]() AC.
AC.
∵点G是AC的中点,
∴CE=AG=EG=AD,
∴∠AEG=∠EAG=30°,
∴∠DAE=30°,
∴∠DAE=∠AEG,
∴AD∥GE,
∴四边形ADEG是菱形.


科目:初中数学 来源: 题型:
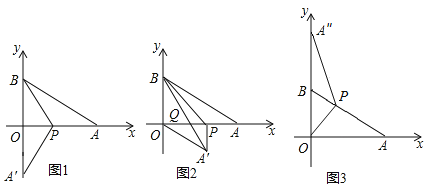
【题目】将一个直角三角形纸片![]() 放置在平面直角坐标系中,点
放置在平面直角坐标系中,点![]() .
.
(1)点![]() 为边
为边![]() 上一点(点
上一点(点![]() 不与
不与![]() 重合),沿
重合),沿![]() 将纸片折叠得
将纸片折叠得![]() 的对应点
的对应点![]() ,边
,边![]() 与
与![]() 轴交于点
轴交于点![]() .
.
①如图1,当点![]() 刚好落在
刚好落在![]() 轴上时,求点
轴上时,求点![]() 的坐标
的坐标
②如图2,当![]() 时,若线段
时,若线段![]() 在
在![]() 轴上移动得到线段
轴上移动得到线段![]() (线段
(线段![]() 平移时
平移时![]() 不动),当△A′O′Q′周长最小时,求OO′的长度.
不动),当△A′O′Q′周长最小时,求OO′的长度.
(2)如图3,若点![]() 为边
为边![]() 上一点(点
上一点(点![]() 不与
不与![]()
![]() 重合),沿
重合),沿![]() 将纸片折叠得
将纸片折叠得![]() 的对应点
的对应点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·湖州)如图,已知抛物线![]() 经过点(0,-3),请你确定一个
经过点(0,-3),请你确定一个
b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间。你确定的b的值是 ▲![]() 。
。
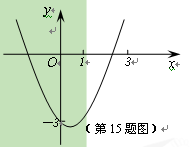
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,AB=8,点E是射线DC上一个动点(点E与点D不重合),连接AE,BE,以BE为边在线段AD的右侧作正方形BEFG,连结CG.
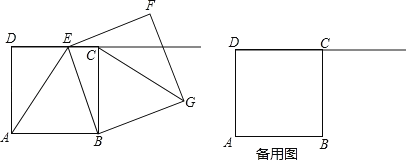
(1)当点E在线段DC上时,求证:△BAE≌△BCG;
(2)在(1)的条件下,若CE=2,求CG的长;
(3)连接CF,当△CFG为等腰三角形时,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为 度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 边上一点.
边上一点.
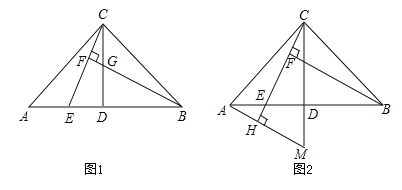
(1)直线![]() 垂直于
垂直于![]() 于点
于点![]() 交
交![]() 于点
于点![]() (如图1),求证
(如图1),求证![]() ;
;
(2)直线![]() 垂直于
垂直于![]() ,垂足为
,垂足为![]() 交
交![]() 的延长线于点
的延长线于点![]() (如图2).求证:
(如图2).求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
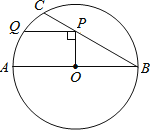
【题目】在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
(1)如图当PQ∥AB时,求PQ的长;
(2)当点P在BC上移动时,线段PQ长的最大值为______;此时,∠POQ的度数为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com