
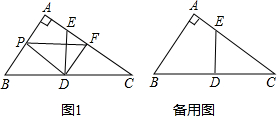
���� ��1��ͨ����ֱ�Ķ��塢ֱ���������е�������ǻ����Լ���������������֤�á�PBM���QNM�е������Ƕ�Ӧ��ȣ�����������������һ�����ƣ�
��2������BP=3�����ݡ�PBD�ס�FEM�Ķ�Ӧ�߳ɱ����������EF�ij�����Fһ�����ƶ��ľ��룬����F���ٶȣ�
�ڷֱ���ʱ��t��ʾ��AP��AF�ij�������ֱ�������ε����������ú�������ʽ��ע����Ҫ�������ۣ���0��t��4ʱ��AP=AB-BP=4$\sqrt{3}$-$\sqrt{3}$t��AF=AE+EF=AC-EC+EF=12-8+t=4+t��Ȼ���������ε������ʽ������øú�����ϵʽ����t��4ʱ��AP=$\sqrt{3}$t-4$\sqrt{3}$��AF=4+t��Ȼ���������ε������ʽ������øú�����ϵʽ��
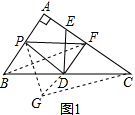
��3��PF2=BP2+CF2�����������ӳ�FD����G��ʹDG=DF������PG��BG����ƽ���ı���BGCF������ƽ���ı��εĶԱ�ƽ���������֪BG��CF��BG=CF��Ȼ����ֱ��������BPG�����ù��ɶ������PG2=BP2+BG2=BP2+CF2����������߶δ�ֱƽ���ߵ�����֪PF=PG�������ɵ�������֤�øý��ۣ�
���  �⣺��1����PBD�ס�FED���������£�
�⣺��1����PBD�ס�FED���������£�
��ͼ1����DF��DP��ME��BC����֪����
���PDB+��PDE=90�㣬��FDE+��PDE=90�㣬
���PDB=��FDE��
�ߡ�PBD+��C=90�㣬��FED+��C=90�㣬
���PBD=��FED��
���PBD�ס�FED��
��2���ߡ�BAC=90�㣬��ABC=60�㣬
��BC=2AB=8$\sqrt{3}$cm��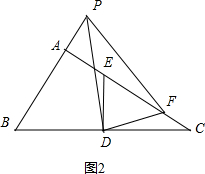
�֡�DE��ֱƽ��BC��
��BD=CD=4$\sqrt{3}$cm��
�ߡ�C=30�㣬
��DE=$\frac{\sqrt{3}}{3}$CD=4cm��
����Q����˶��ٶ�Ϊvcm/s��
��ͼ1����0��t��4ʱ���ɣ�1��֪��PBD�ס�FED��
��$\frac{EF}{BP}$=$\frac{DE}{DB}$����$\frac{vt}{\sqrt{3}t}$=$\frac{4}{4\sqrt{3}}$��
��v=1��
��ͼ2����t��4ʱ��ͬ���ɵ�v=1��
����������Q���˶��ٶ�Ϊ1cm/s��
�ڡ�AE=AC-EC=12-8=4cm��
����ͼ1����0��t��4ʱ��AP=AB-BP=4$\sqrt{3}$-$\sqrt{3}$t��AF=AE+EF=AC-EC+EF=12-8+t=4+t��
��S=$\frac{1}{2}$AP•AF=$\frac{1}{2}$��4$\sqrt{3}$-$\sqrt{3}$t����4+t��=-$\frac{\sqrt{3}}{2}$t2+8$\sqrt{3}$��
��ͼ2����t��4ʱ��AP=$\sqrt{3}$t-4$\sqrt{3}$��AQ=4+t��
��S=$\frac{1}{2}$AP•AQ=$\frac{1}{2}$��$\sqrt{3}$t-4$\sqrt{3}$����4+t��=$\frac{\sqrt{3}}{2}$t2-8$\sqrt{3}$��
����������S=$\left\{\begin{array}{l}{-\frac{\sqrt{3}}{2}{t}^{2}+8\sqrt{3}��0��t��4��}\\{\frac{\sqrt{3}}{2}{t}^{2}-8\sqrt{3}��t��4��}\end{array}\right.$��
��3��PF2=BP2+CF2��
֤�����£���ͼ1���ӳ�FD����G��ʹDG=DF������PG��BG��BF��CG
��BC��GF����ƽ�֣�
���ı���BGCFΪƽ���ı��Σ�
��BG��CF��BG=CF��ƽ���ı��εĶԱ�ƽ������ȣ���
�֡ߡ�BAC=90�㣬
���PBG=90�㣬
��PG2=BP2+BG2=BP2+CF2��
��PD��ֱƽ��GF��
��PF=PG��
��PF2=BP2+CF2��
���� ���⿼�������������ε��ж������ʣ��Լ������������뺯�����ۺ�Ӧ�ã�����ʱ��t��ȷ��ʾ����Ŀ���߶εij����ǽ���Ĺؼ���


 �Ƹ�С״Ԫ���ֳ������ϵ�д�
�Ƹ�С״Ԫ���ֳ������ϵ�д� �¸��̵�ѧϵ�д�
�¸��̵�ѧϵ�д� ����ͬѧһ����ʦȫ�źþ�ϵ�д�
����ͬѧһ����ʦȫ�źþ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ���ھ���ABCD�У�AB=12cm��BC=6cm����P��AB�ߴӵ�A��ʼ���B��2cm/s���ٶ��ƶ�����Q��DA�ߴӵ�D���A��1cm/s���ٶ��ƶ������P��Qͬʱ��������t��s����ʾ�ƶ�ʱ�䣨0��t��6������ô��
��ͼ��ʾ���ھ���ABCD�У�AB=12cm��BC=6cm����P��AB�ߴӵ�A��ʼ���B��2cm/s���ٶ��ƶ�����Q��DA�ߴӵ�D���A��1cm/s���ٶ��ƶ������P��Qͬʱ��������t��s����ʾ�ƶ�ʱ�䣨0��t��6������ô���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | -1 | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com