
分析 作出图形,根据直线解析式求出OA、OB,利用勾股定理列式求出AB,过点C作CD⊥AB于D,根据角平分线上的点到角的两边距离相等可得OC=CD,设OC=y,用∠ABO的正弦表示出BC,然后根据OB的长度列方程求解即可.
解答 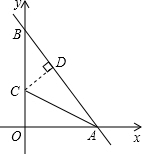 解:如图,令y=0,则-$\frac{4}{3}$x+8=0,
解:如图,令y=0,则-$\frac{4}{3}$x+8=0,
解得x=6,
所以,OA=6,
令x=0,则y=8,
所以,OB=8,
由勾股定理得,AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
过点C作CD⊥AB于D,
∵AC平分∠OAB,
∴OC=CD,
设OC=y,
则CD=x,
BC=CD÷sin∠ABO=y÷$\frac{6}{10}$=$\frac{5}{3}$y,
∵OB=OC+BC=y+$\frac{5}{3}$y=$\frac{8}{3}$y,
∴$\frac{8}{3}$y=8,
解得y=3,
即OC=3.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,勾股定理,一次函数图象上点的坐标特征,熟记各性质是解题的关键,作出图形更形象直观.


科目:初中数学 来源: 题型:选择题
| A. | y随x的增大而减小 | B. | 图象位于一、三象限 | ||
| C. | 图象是轴对称图形 | D. | 点(-1,-2)在这个图象上 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 2014年,山西省某地实施了“免费校车工程”.小明原来骑自行车上学,现在乘校车上学可以从家晚10分钟出发,结果与原来到校时间相同.已知小明家距学校5千米,若校车速度是他骑车速度的2倍,设小明骑车的速度为x千米/小时,则所列方程正确的为( )
2014年,山西省某地实施了“免费校车工程”.小明原来骑自行车上学,现在乘校车上学可以从家晚10分钟出发,结果与原来到校时间相同.已知小明家距学校5千米,若校车速度是他骑车速度的2倍,设小明骑车的速度为x千米/小时,则所列方程正确的为( )| A. | $\frac{5}{x}$+$\frac{1}{6}$=$\frac{5}{2x}$ | B. | $\frac{5}{x}$=$\frac{5}{2x}$+$\frac{1}{6}$ | C. | $\frac{5}{x}$+10=$\frac{5}{2x}$ | D. | $\frac{5}{x}$-10=$\frac{5}{2x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
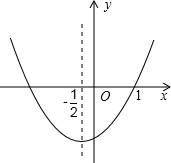 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=-$\frac{1}{2}$,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=-$\frac{1}{2}$,有下列结论:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com