
【题目】已知:一次函数y=3x-2的图象与某反比例函数的图象的一个公共点的横坐标为1.
(1)(3分)求该反比例函数的解析式;
(2)(3分)将一次函数y=3x-2的图象向上平移4个单位,求平移后的图象与反比例函数图象的交点坐标;
(3)(2分)请直接写出一个同时满足如下条件的函数解析式:
①函数的图象能由一次函数y=3x-2的图象绕点(0,-2)旋转一定角度得到;
②函数的图象与反比例函数的图象没有公共点.
【答案】(1)![]() (2)交点坐标为(
(2)交点坐标为(![]() ,3)和(-1, -1) (3)y=-2x-2(答案不唯一)
,3)和(-1, -1) (3)y=-2x-2(答案不唯一)
【解析】
解:(1)把x=1代入y=3x-2,得y=1。
设反比例函数的解析式为![]() ,把(1,1)代入得,k=1。
,把(1,1)代入得,k=1。
∴该反比例函数的解析式为![]()
(2)平移后的图象对应的解析式为y=3x-2+4,即y=3x+2,
联立y=3x+2和![]() ,得,
,得,
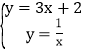 ,解得
,解得![]() 或
或![]() 。
。
∴平移后的图象与反比例函数图象的交点坐标为(![]() ,3)和(-1, -1) 。
,3)和(-1, -1) 。
(3)y=-2x-2(答案不唯一)。
(1)先求出两函数的交点坐标,利用待定系数法即可求得反比例函数的解析式。
(2)平移后的图象对应的解析式为y=3x+2,联立两函数解析式,从而求得交点坐标。
(3)∵函数的图象由一次函数y=3x-2的图象绕点(0,-2)旋转一定角度得到,
∴可设所求函数解析式为y=mx-2,则由
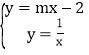 得
得![]() 。
。
∵函数的图象与反比例函数的图象没有公共点,
∴△=4-4·m(-1)<0,解得m<-1。
∴只要常数项为-2,一次项系数小于-1的一次函数均可。


科目:初中数学 来源: 题型:
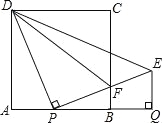
【题目】如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q.
(1)求线段PQ的长;
(2)问:点P在何处时,△PFD∽△BFP,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为锐角,点
为锐角,点![]() 为直线
为直线![]() 上一动点,以
上一动点,以![]() 为直角边且在
为直角边且在![]() 的右侧作等腰直角三角形
的右侧作等腰直角三角形![]() ,
,![]() ,
,![]() .
.

(1)如果![]() ,
,![]() .
.
①当点![]() 在线段
在线段![]() 上时,如图1,线段
上时,如图1,线段![]() 、
、![]() 的位置关系为___________,数量关系为_____________
的位置关系为___________,数量关系为_____________
②当点![]() 在线段
在线段![]() 的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.
的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.
(2)如图3,如果![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动。探究:当
上运动。探究:当![]() 多少度时,
多少度时,![]() ?小明通过(1)的探究,猜想
?小明通过(1)的探究,猜想![]() 时,
时,![]() .他想过点
.他想过点![]() 做
做![]() 的垂线,与
的垂线,与![]() 的延长线相交,构建图2的基本图案,寻找解决此问题的方法。小明的想法对吗?如不对写出你的结论;如对按此方法解决问题并写出理由.
的延长线相交,构建图2的基本图案,寻找解决此问题的方法。小明的想法对吗?如不对写出你的结论;如对按此方法解决问题并写出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据媒体报道,2月29日,包括普通口罩、医用口罩、医用N95口罩在内,全国口罩日产能达到1.1亿只,日产量达到1.16亿只,分别是2月1日的52倍、12倍,进一步缓解了口罩供需矛盾,虽然还不能满足国内需求,但还是积极支援一些其他困难国家.日产量1.16亿用科学记数法表示为( )
A.1.16×1010B.11.6×109C.1.16×108D.1.6×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,∠A=∠D,说明∠F与∠C相等的理由.
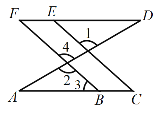
解:∵∠1=∠2( 已知 ),∠2=∠4 ( ),
∴∠1=∠4( 等量代换 ),
∴FB∥EC( ),
∴∠3=∠C( 两直线平行,同位角相等 ).
∵∠A=∠D( ),
∴ED∥AC( ),
∴∠F=∠3 ( ),
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知等腰三角形的一边长等于8cm,一边长等于9cm,求它的周长;
(2)等腰三角形的一边长等于6cm,周长等于28cm,求其他两边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
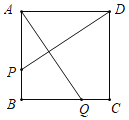
【题目】如图,在正方形ABCD中,AB=8厘米,如果动点P在线段AB上以2厘米/秒的速度由A点向B点运动,同时动点Q在以1厘米/秒的速度线段BC上由C点向B点运动,当点P到达B点时整个运动过程停止.设运动时间为t秒,当AQ⊥DP时,t的值为_____秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
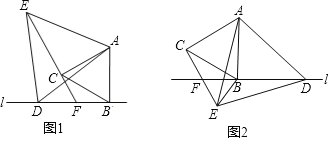
【题目】已知线段AB⊥直线l于点B,点D在直线l上,分别以AB,AD为边作等边三角形ABC和等边三角形ADE,直线CE交直线l于点F
(1)当点F在线段BD上时,如图1,线段DF,CE,CF之间的数量关系是 ;
(2)当点F在线段DB的延长线上时,如图2.
①(1)中的数量关系是否仍然成立?若成立,请写出证明过程;若不成立,请重新写出正确的结论,并写出证明过程;
②若等边△ABC和等边△ADE的边长分别是![]() 和
和![]() ,DF=3,求BE的长.
,DF=3,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com