
【题目】已知∠AOB=70°,∠AOD=![]() ∠AOC,∠BOD=3∠BOC(∠BOC<45°),则∠BOC的度数是______.
∠AOC,∠BOD=3∠BOC(∠BOC<45°),则∠BOC的度数是______.
【答案】10°或14°或30°或42°
【解析】
①当射线OC在∠AOB内部时,此时射线OD的位置只有两种可能:i)若射线OD在∠AOC内部,ii)若射线OD在∠AOB外部,
②当射线OD在∠AOB外部时,i)若射线DO在∠AOB内部,ii)若射线OD在∠AOB外部分别求出即可.
解:设∠BOC=α,
∴∠BOD=3∠BOC=3α,
依据题意,分两种情况:
①当射线OC在∠AOB内部时,此时射线OD的位置只有两种可能:
i)若射线OD在∠AOC内部,如图2,
∴∠COD=∠BOD-∠BOC=2α,
∵∠AOD=![]() ∠AOC,
∠AOC,
∴∠AOD=∠COD=2α,
∴∠AOB=∠AOD+∠BOD=2α+3α=5α=70°,
∴α=14°,
∴∠BOC=14°;
ii)若射线OD在∠AOB外部,如图3,
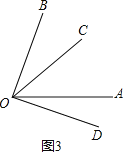
∴∠COD=∠BOD-∠BOC=2α,
∵∠AOD=![]() ∠AOC,
∠AOC,
∴∠AOD=![]() ∠COD=
∠COD=![]() α,
α,
∴∠AOB=∠BOD-∠AOD=3α-![]() α=
α=![]() α=70°,
α=70°,
∴α=30°,
∴∠BOC=30°;
②当射线OD在∠AOB外部时,
依据题意,此时射线OC靠近射线OB,
∵∠BOC<45°,∠AOD=![]() ∠AOC,
∠AOC,
∴射线OD的位置也只有两种可能:
i)若射线DO在∠AOB内部,如图4,
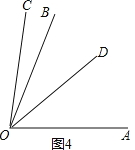
则∠COD=∠BOC+∠BOD=4α,
∵∠AOD=![]() ∠AOC,
∠AOC,
∴∠AOD=∠COD=4α,
∴∠AOB=∠BOD+∠AOD=4α,
∴AOB=∠BOD+∠AOD=3α+4α=7α=70°,
∴α=10°,
∴∠BOC=10°
ii)若射线OD在∠AOB外部,如图5,

则∠COD=∠BOC+∠DOB=4α,
∵∠AOD=![]() ∠AOC,
∠AOC,
∴∠AOD=![]() ∠COD=
∠COD=![]() α,
α,
∴∠AOB=∠BOD-∠AOD=3α-![]() α=
α=![]() α=70°,
α=70°,
∴α=42°,
∴∠BOC=42°,
综上所述:∠BOC的度数分别是10°,14°,30°,42°.
故答案为:10°或14°或30°或42°


科目:初中数学 来源: 题型:
【题目】(1)![]() ﹣(+9)﹣12﹣(
﹣(+9)﹣12﹣(![]() )
)
(2)4﹣2×(﹣3)2+6÷(﹣![]() )
)
(3)化简:5(a2+5a)﹣(a2+7a)
(4)先化简,再求值:2(a2b+ab2)﹣3(a2b﹣1)﹣2ab2﹣4,其中a=2018,b=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要测量河岸相对的两点A、B之间的距离,先从B处出发与AB成![]() 方向,向前走50米到C处立一根标杆,然后方向不变继续朝前走50米到D处,在D处转
方向,向前走50米到C处立一根标杆,然后方向不变继续朝前走50米到D处,在D处转![]() 沿DE方向再走17米,到达E处,此时A、C、E三点在同一直线上,那么A、B两点间的距离为
沿DE方向再走17米,到达E处,此时A、C、E三点在同一直线上,那么A、B两点间的距离为![]()
![]()
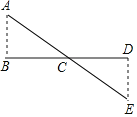
A. 10米 B. 12米 C. 15米 D. 17米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮玩一个游戏:取三张大小、质地都相同的卡片,上面分别标有数字2,3,4(背面完全相同),现将标有数字的一面朝下.小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和.
(1)请你用画树状图或列表的方法,求出这两数和为6的概率.
(2)如果和为奇数,则小明胜;若和为偶数,则小亮胜.你认为这个游戏规则对双方公平吗?做出判断,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB表示一条对折的绳子,现从P点将绳子剪断.剪断后的各段绳子中最长的一段为30cm.若AP=![]() BP,則原来绳长为( )cm.
BP,則原来绳长为( )cm.
![]()
A. 55cmB. 75cmC. 55或75cmD. 50或75cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c为△ABC的三条边的长,且满足b2+2ab=c2+2ac.
(1)试判断△ABC的形状,并说明理由;
(2)若a=6,b=5,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知a+b=﹣![]() ,求代数式(a﹣1)2+b(2a+b)+2a的值.
,求代数式(a﹣1)2+b(2a+b)+2a的值.
(2)已知a,b,c是三角形的三边,且a2+b2+c2﹣ab﹣bc﹣ac=0.求证:此三角形是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,是一个长为 2m,宽为 2n 的长方形,沿图中虚线用剪刀将其均分成四个完全相同的小长方形,然后按图 2 的形状拼图.
(1)图 2 中的图形阴影部分的边长为 ;(用含 m、n 的代数式表示)
(2)请你用两种不同的方法分别求图 2 中阴影部分的面积; 方法一: ;方法二: .
(3)观察图 2,请写出代数式(m+n)2、(m﹣n)2、4mn 之间的关系式: .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com