
 如图,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,点D为抛物线的顶点,点P为第一象限抛物线上一点,且∠DAP=45°,求点P的坐标.
如图,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,点D为抛物线的顶点,点P为第一象限抛物线上一点,且∠DAP=45°,求点P的坐标. 分析 如图所示构造△AKD全等△DNM,先求得点A和点D的坐标,从而可求得点M的坐标,最后求得直线AM的坐标即可.
解答 解:如图所示:构造△AKD≌△DNM,连接AM.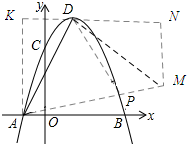
将y=0代入抛物线的解析式得:-x2+2x+3=0.
解得:x1=3,x2=-1.
∴点A的坐标为(-1,0).
∴点D的横坐标为1.
将x=1代入抛物线的解析式得y=4.
∴AK=4,KD=2,∴DN=4,NM=2.
∴点M的坐标为(5,2).
设直线AM的解析式y=kx+b.将点A、点M的解析式代入得:$\left\{\begin{array}{l}{-k+b=0}\\{5k+b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{3}}\\{b=\frac{1}{3}}\end{array}\right.$.
∴直线AM的解析式为y=$\frac{1}{3}x+\frac{1}{3}$.
将y=$\frac{1}{3}x+\frac{1}{3}$与y=-x2+2x+3联立.
解得:x=$\frac{8}{3}$,y=$\frac{11}{9}$或x=-1,y=0(舍去).
∴点P的坐标为($\frac{8}{3}$,$\frac{11}{9}$).
点评 本题主要考查的是二次函数的综合应用,一次函数的图象和性质、解二元二次方程组,构造△AKD≌△DNM是解题的关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
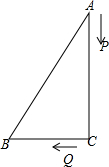 如图,Rt△ABC中,∠C=90°,BC=a,AC=b(a<b),AB=5,a,b是方程x2-(m-1)x+(m+4)=0的两根
如图,Rt△ABC中,∠C=90°,BC=a,AC=b(a<b),AB=5,a,b是方程x2-(m-1)x+(m+4)=0的两根查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
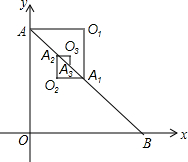 如图,在Rt△AOB中,OA=OB=1,取AB的中点A1,以AA1为斜边作等腰直角三角形AO1A1,取AA1的中点A2,以A1A2为斜边作等腰直角三角形A1O2A1;取A1A2的中点A3,以A2A3为斜边作等腰直角三角形A2O3A3…,则点O6的坐标是($\frac{21}{64}$,$\frac{21}{32}$).
如图,在Rt△AOB中,OA=OB=1,取AB的中点A1,以AA1为斜边作等腰直角三角形AO1A1,取AA1的中点A2,以A1A2为斜边作等腰直角三角形A1O2A1;取A1A2的中点A3,以A2A3为斜边作等腰直角三角形A2O3A3…,则点O6的坐标是($\frac{21}{64}$,$\frac{21}{32}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
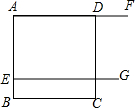 如图,正方形ABCD的边长是4,E是AB上一点,F是AD延长线上的一点,BE=DF,四边形AEGF是矩形,矩形AEGF的面积y随BE的长x的变化而变化,y与x之间的关系可以用怎样的函数来表示?
如图,正方形ABCD的边长是4,E是AB上一点,F是AD延长线上的一点,BE=DF,四边形AEGF是矩形,矩形AEGF的面积y随BE的长x的变化而变化,y与x之间的关系可以用怎样的函数来表示?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
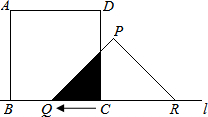 如图,有一边长为5cm的正方形ABCD和等腰Rt△PQR,QR=8cm,点B、C、Q、R在同一条直线上,当C、Q两点重合时,△PQR以1cm/秒的速度向左开始匀速运动,设与正方形重合部分的面积为S cm2.
如图,有一边长为5cm的正方形ABCD和等腰Rt△PQR,QR=8cm,点B、C、Q、R在同一条直线上,当C、Q两点重合时,△PQR以1cm/秒的速度向左开始匀速运动,设与正方形重合部分的面积为S cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
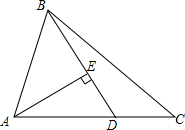 如图,△ABC中,∠BCA=45°,点D在AC上,∠BDA=60°,AD=2DC,AE⊥BD于E.求证:
如图,△ABC中,∠BCA=45°,点D在AC上,∠BDA=60°,AD=2DC,AE⊥BD于E.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com