
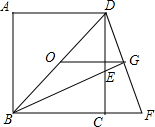
 已知:如图,O为正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG.
已知:如图,O为正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG.分析 (1)根据正方形的性质和全等三角形的判定定理证明;
(2)根据等腰三角形的三线合一得到DG=GF,根据三角形中位线定理解答;
(3)设BC=x,用x表示出CF,利用勾股定理表示出DF,证明△DGE∽△BGD,根据相似三角形的性质得到DG2=GE•GB,计算即可.
解答 (1)证明:在正方形ABCD中,BC=CD,∠BCD=90°.
在BCE和△DCF中,
$\left\{\begin{array}{l}{BC=DC}\\{∠BCE=∠DCF}\\{CE=CF}\end{array}\right.$,
∴△BCE≌△DCF;
(2)解:OG=$\frac{1}{2}$BF.
∵△BCE≌△DCF,
∴∠EBC=∠FDC,
∵∠BEC=∠DEG,
∴∠DGE=∠BCE=90°,即BG⊥DF.
∵BE平分∠DBC,
∴BD=BF,G为DF的中点.
∵O为正方形ABCD的中心,
∴O为BD的中点.
∴OG=$\frac{1}{2}$BF;
(3)解:设BC=x,则DC=x,BD=$\sqrt{2}$x,
由(2),得BF=BD=$\sqrt{2}$x.
∴CF=BF-BC=($\sqrt{2}$-1)x.
在Rt△DCF中,
DF2=DC2+CF2=x2+($\sqrt{2}$-1)2x2,
∵∠GDE=∠GBC=∠GBD,∠DGE=∠BGD=90°,
∴△DGE∽△BGD,
∴$\frac{DG}{GB}$=$\frac{GE}{DG}$,
即DG2=GE•GB=4-2$\sqrt{2}$,
∵DF=2DG,
∴DF2=4DG2=4(4-2$\sqrt{2}$),
则x2+($\sqrt{2}$-1)2x2=4(4-2$\sqrt{2}$).
解得x2=4.
∴正方形ABCD的面积为4.
点评 本题考查的是正方形的性质、等腰三角形的性质、全等三角形的判定定理和性质定理、相似三角形的性质定理以及勾股定理的应用,掌握等腰三角形的三线合一以及相似三角形的判定定理和性质定理是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
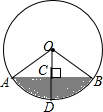 将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯的半径是4cm,水面宽度AB是4$\sqrt{3}$cm.
将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯的半径是4cm,水面宽度AB是4$\sqrt{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
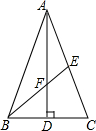 如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AD=18,点E在AC上且CE=$\frac{1}{2}$AC,连接BE,与AD相交于点F.若BE=15,则△DBF的周长是24.
如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AD=18,点E在AC上且CE=$\frac{1}{2}$AC,连接BE,与AD相交于点F.若BE=15,则△DBF的周长是24.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
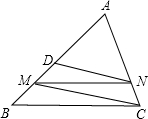 如图,在△ABC中,点M在边AB上,过点M作MN∥BC交AC于N,过点N作DN∥MC交AB于D.已知AB=4,AM=3,则AD的长为$\frac{9}{4}$.
如图,在△ABC中,点M在边AB上,过点M作MN∥BC交AC于N,过点N作DN∥MC交AB于D.已知AB=4,AM=3,则AD的长为$\frac{9}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com